Definition. Zwei Punktepaare $A,B$ und $C,D$ auf einer Geraden liegen harmonisch, wenn gilt
$$
\frac{\overset{\longrightarrow}{CA}}{\overset{\longrightarrow}{CB}} = -\frac{\overset{\longrightarrow}{DA}}{\overset{\longrightarrow}{DB}}.
$$
Definition. Ein vollständiges Vierseit besteht aus vier verschiedenen Geraden $ g_0 ,\, g_1 ,\, g_2 ,\, g_3$ in der Ebene, die sich paarweise schneiden, von denen jedoch keine drei durch ein und denselben Punkt gehen.
Satz 5.11. In einem vollständigen Vierseit seien $A,B$ zwei Eckpunkte, die nicht beide auf einer Seite liegen. Die Diagonale $AB$ möge von den anderen beiden Diagonalen in den Punkten $C,D$ geschnitten werden. Dann liegen die Punkte $A,B$ und $C,D$ harmonisch. 
Beweis. Wir wählen uns einen weiteren Eckpunkt $E$ des Vierseits. Die Sätze von Menelaos und Ceva werden beide auf das Dreieck $ABE$ angewandt. Die Eckpunkte $A'$ und $B'$ sind die jeweils dritten Eckpunkte des Vierseits auf den Geraden $BE$ und $AE$.
Der Satz des Ceva mit $C$ in der Rolle von $E'$ liefert die Gleichung
$$
\frac{\overset{\longrightarrow}{A'B}}{\overset{\longrightarrow}{A'E}}
\cdot
\frac{\overset{\longrightarrow}{B'E}}{\overset{\longrightarrow}{B'A}}
\cdot
\frac{\overset{\longrightarrow}{CA}}{\overset{\longrightarrow}{CB}}
= -1.
$$
Aus dem Satz des Menelaos mit $D$ in der Rolle des $E'$ ergibt:
$$
\frac{\overset{\longrightarrow}{A'B}}{\overset{\longrightarrow}{A'E}}
\cdot
\frac{\overset{\longrightarrow}{B'E}}{\overset{\longrightarrow}{B'A}}
\cdot
\frac{\overset{\longrightarrow}{DA}}{\overset{\longrightarrow}{DB}}
= 1.
$$ Die Harmoniebedingung folgt unmittelbar nach Kürzen der jeweils beiden ersten Faktoren.
qed.
Lemma des Apollonius 5.12. Es sei $ASB$ ein Dreieck. Es sei $C \in \overline{AB}$ der Schnittpunkt der Winkelhalbierenden durch $S$ mit der Seite $AB$. Die Senkrechte zu $SC$ durch $S$ schneide die Gerade $AB$ in $D$. Dann liegen die Punktepaare $AB$ und $ CD$ harmonisch.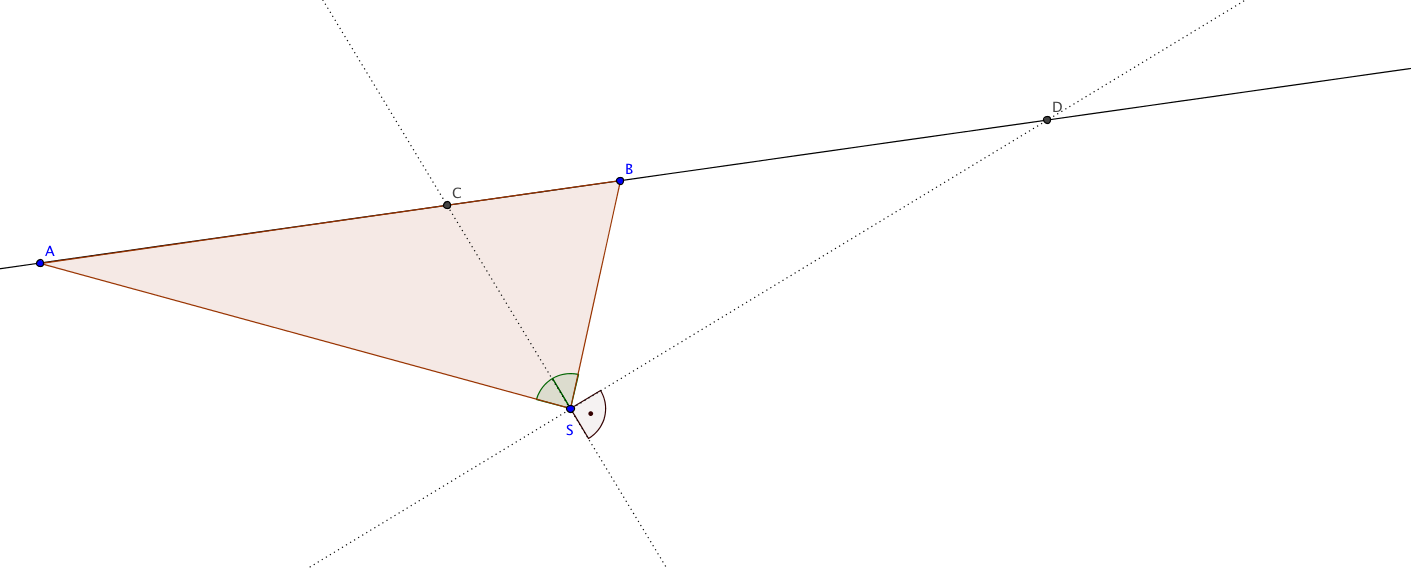
Beweis. Man zieht eine Parallele zur Geraden $SD$ durch den Punkt $B$. Der Schnittpunkt mit $AS$ sei $E$.
Dann ist $BE$ senkrecht zu $SC$, da $SD$ senkrecht zu $SC$ war. Man findet $|ES| =
|BS|$, denn dies sind die Hypothenusen zweier kongruenter rechwinkliger Dreiecke. Aus dem Strahlensatz, angewandt auf die Parallelen $EB$ und $SD$, ergibt sich:
$$
\frac{|AD|}{|BD|} = \frac{|AS|}{|ES|} = \frac{|AS|}{|BS|}.
$$ Andererseits findet man nach dem Satz (5.10) über die Winkelhalbierende:
$$
\frac{|AS|}{|BS|} = \frac{|AC|}{|BC|}
$$ Zusammen mit der letzten Gleichnung ergibt sich, dass die Punkte $A,B$ und $C,D$ harmonisch liegen:
$$
\frac{|AD|}{|BD|} = \frac{|AC|}{|BC|}.
$$qed.
Es seien $g$, $g'$ und $h$ paarweise verschiedene parallele Geraden und Punkte $A\in g$ und $A'\in g'$ vorgegeben. Wir definieren eine Abbildung $p: g \rightarrow g'$ mittels folgender Konstruktion. Man setzt $p(A) = A'$. Für einen Punkt $B \in g$ sei $B_h$ der Schnittpunkt der Geraden $A'B$ mit $h$ und $B'$ der Schnittpunkt von $AB_h$ mit der Geraden $g'$. Wir setzen $$
p(B) = B'.
$$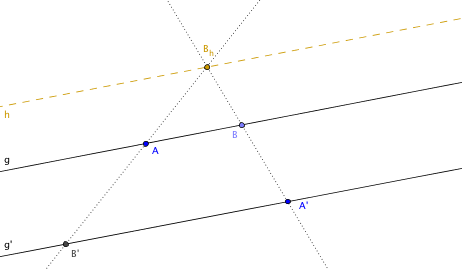
Vierter Strahlensatz 5.13. Die Abbildung $p$ ist affin.
Beweis. Wir unterscheiden zwei Fälle. Im ersten Fall verläuft die Gerade $h$ genau in der Mitte zwischen $g$ und $g'$.
In diesem Fall liefert der zweite Strahlensatz $$\frac{\overrightarrow{A'B'}}{\overrightarrow{BA}}=\frac{\overrightarrow{B_hA'}}{\overrightarrow{B_hB}}=-1.$$ Insbesondere gilt $|AB|=|A'B'|$. Das Viereck $AA'B'B$ ist also nach (4.1) ein Parallelogramm und folglich $p$ eine Parallelprojektion entlang der Geraden $AA'$. Aus dem ersten Strahlensatz folgt, dass $p$ affin ist.
Im allgemeinen Fall sei $C$ der Schnittpunkt von $h$ mit $AA'$. Die Strahlensätze liefern $$\frac{\overrightarrow{B'A'}}{\overrightarrow{BA}}=-\frac{\overrightarrow{B'A'}}{\overrightarrow{AB}}=-\frac{\overrightarrow{B_hA'}}{\overrightarrow{B_hB}}=-\frac{\overrightarrow{CA'}}{\overrightarrow{CA}}.$$
Es gibt einen eindeutig bestimmten Punkt $D$ auf der Geraden $AA'$, so dass die Punktepaare $A,A'$ und $C,D$ harmonisch liegen. Zentralprojektion mit Zentrum $D$ bildet den Punkt $B$ auf einen Punkt $B_D'\in g'$ ab, der die Gleichung $$\frac{\overrightarrow{B_D'A'}}{\overrightarrow{BA}}=\frac{\overrightarrow{DA'}}{\overrightarrow{DA}}$$ erfüllt. Wegen der Harmoniebedingung $$ \frac{\overset{\longrightarrow}{CA}}{\overset{\longrightarrow}{CA'}} = -\frac{\overset{\longrightarrow}{DA}}{\overset{\longrightarrow}{DA'}}$$ folgt also $$ \frac{\overrightarrow{B_D'A'}}{\overrightarrow{BA}}=\frac{\overrightarrow{B'A'}}{\overrightarrow{BA}}$$ und damit $B_D'=B'$. Die Abbildung $p$ ist folglich gleich der Zentralprojektion mit Zentrum $D$, nach dem dritten Strahlensatz also affin.
qed.
Den im Beweis auftauchende Punkt $D$ lässt sich übrigens, wie in der Vorlesung vorgeführt, mittels eines vollständigen Vierseits nach (5.11) explizit konstruieren.