Satz vom Zentriwinkel 7.1. Es sei $\overline{AB}$ eine Sehne in einem Kreis $\mathcal{K}$ und $C \in \mathcal{K}\setminus \{A,B\}$ ein Punkt, der auf der gleichen Seite der Geraden $AB$ liegt wie der Mittelpunkt $M$ von $\mathcal{K}$. Dann gilt
$$
2 \sphericalangle ACB = \sphericalangle AMB.
$$
Beweis. Es sei $\overline{BC'}$ der Kreisdurchmesser. Nach dem Peripheriewinkelsatz 4.9 gilt $$\sphericalangle ACB=\sphericalangle AC'B.$$ Andererseits ist $AC'M$ ein gleichschenkliges Dreieck. Folglich gilt $$\angle AC'B=\angle AC'M=\angle MAC'.$$ Aus der Winkelsumme des Dreiecks erhält man $$180°-2\angle AC'M=\angle AMC'=180°-\angle AMB.$$ 
Die Aussage folgt unmittelbar.
qed.
Korollar 7.2. Es es $ABC$ ein Dreieck. Die Mittelsenkrechte auf die Seite $\overline{BC}$ schneide den Umkreis im Punkte $D$. Dann gilt:
Beweis. Nach dem Zentriwinkelsatz bezüglich der Sehne $BC$ ist der Winkel $\angle CMB$ doppelt so groß wie der Winkel $\angle CAB$. Die Gerade $MD$ halbiert den Winkel $\angle CMB$. Wiederum nach dem Zentriwinkelsatz, diesmal bezüglich der Sehne $DC$, halbiert die Strecke $AD$ den Winkel $\angle CAD$. 
Für die zweite Aussage betrachten wir zuerst das Dreieck $BCD$. Spiegelung an der Mittelsenkrechten $MD$ bildet es auf sich selbst ab. Insbesondere gilt die erste Gleichung $|BD|=|CD|$. Zum Beweis der zweiten Gleichung müssen wir das Dreieck $CDI$ als gleichschenklig nachweisen. Dazu betrachten wir die Innenwinkel bei $C$ und $I$.
Der Punkt $I$ ist Schnittpunkt der Winkelhalbierenden. Wegen der Winkelsumme im Dreieck $AIC$ gilt $$\angle CID = \frac12\left( \angle CAB + \angle BCA\right).$$ Der Winkel $\angle DCB$ ist einer der beiden gleichen Winkel im gleichschenkligen Dreieck $BCD$. Der dritte Winkel in diesem Dreieck ergänzt sich nach dem Peripheriewinkelsatz mit dem Winkel $\angle CAB$ zu $180°$. Folglich ist $\angle DCB=\angle CAD$ und damit $\angle DCI=\angle CID$.
qed.
Sind von einem Dreieck zum Beispiel ein Eckpunkt $A$, sowie Mittelpunkte $I$ und $U$ von In- und Umkreis bekannt, so lässt sich mittels dieses Korollars das Dreieck recht einfach rekonstruieren: Der Kreis um $M$, welcher durch $A$ geht, ist der Umkreis. Die Gerade $AI$ ist eine Winkelhalbierende im gesuchten Dreieck $ABC$ und schneidet den Umkreis in einem weiteren Punkt $D$. Die Eckpunkte $B$ und $C$ erhält man als Durchschnitt des Umkreises mit dem Kreis um $D$ durch $I$.
Satz des Pythagoras 7.3. Es sei $ABC$ ein rechtwinkliges Dreieck mit der Hypotenuse $c=|AB|$ und den Katheten $a=|BC|$ und $b=|AC|$. Dann gilt:
$$c^2=a^2+b^2.$$
Beweis. Wir legen uns vier Kopien des Dreiecks, wie in der Graphik angedeutet, aneinander, so dass die Hypotenusen der vier Dreiecke ein Quadrat mit Seitenlänge $c$ und Fläche $c^2$ formen.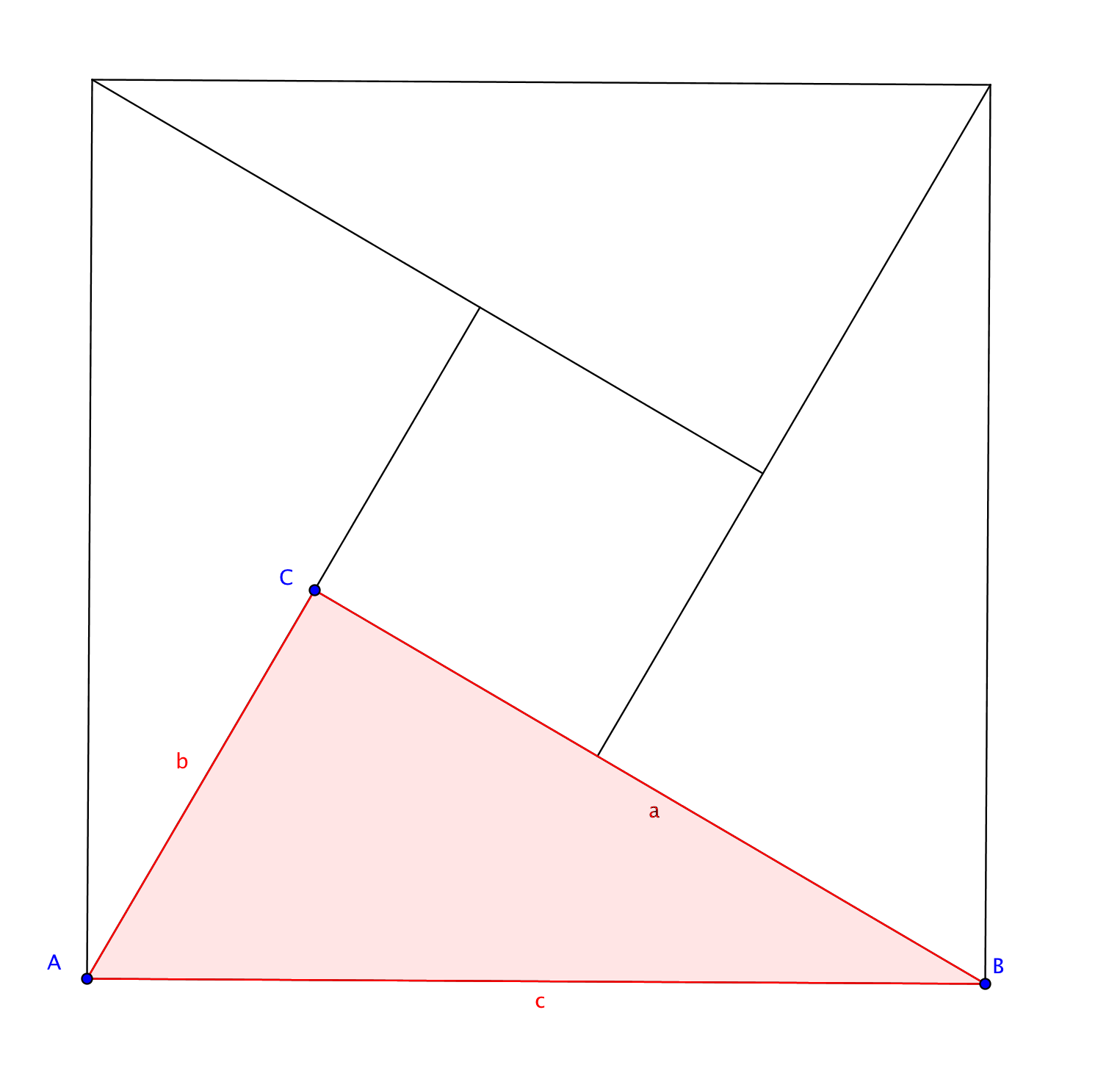
Die Fläche des rechtwinkligen Dreiecks $ABC$ lässt sich berechnen als $\frac12ab$. Legen wir nämlich ein um 180° gedrehtes Exemplar entlang der Hypotenuse an das Dreieck, so erhalten wir ein Rechteck mit Kantenlängen $ a$ und $b$, also der Fläche $ab$.
Die vier Kopien unseres rechtwinkligen Dreiecks überdecken nicht das ganze Quadrat mit Seitenlänge $c$. Es bleibt ein kleines Quadrat mit Seitenlänge $ |a-b|$ und Fläche $(a-b)^2$ frei. Die Fläche des großen Quadrats ist gleich der Summe der Flächen der vier rechtwinkligen Dreiecke, sowie der Fläche des kleinen Quadrats. In Formeln ausgedrückt, $$c^2=4 \left(\frac12 ab\right)+ (a-b)^2=2ab+(a^2-2ab+b^2)=a^2+b^2.$$qed.
Definition. Es sei $ABC$ ein Dreieck mit rechtem Winkel im Punkte $C$. Es sei $\alpha$ der Winkel bei $A$. Der Kosinus von $\alpha$ ist definiert als das Verhältnis $$\cos\alpha=\frac{|AC|}{|AB|}$$ von Ankathete und Hypotenuse. Der Sinus von $\alpha$ ist das Verhältnis $$\sin\alpha=\frac{|BC|}{|AB|}$$ von Gegenkathete und Hypotenuse.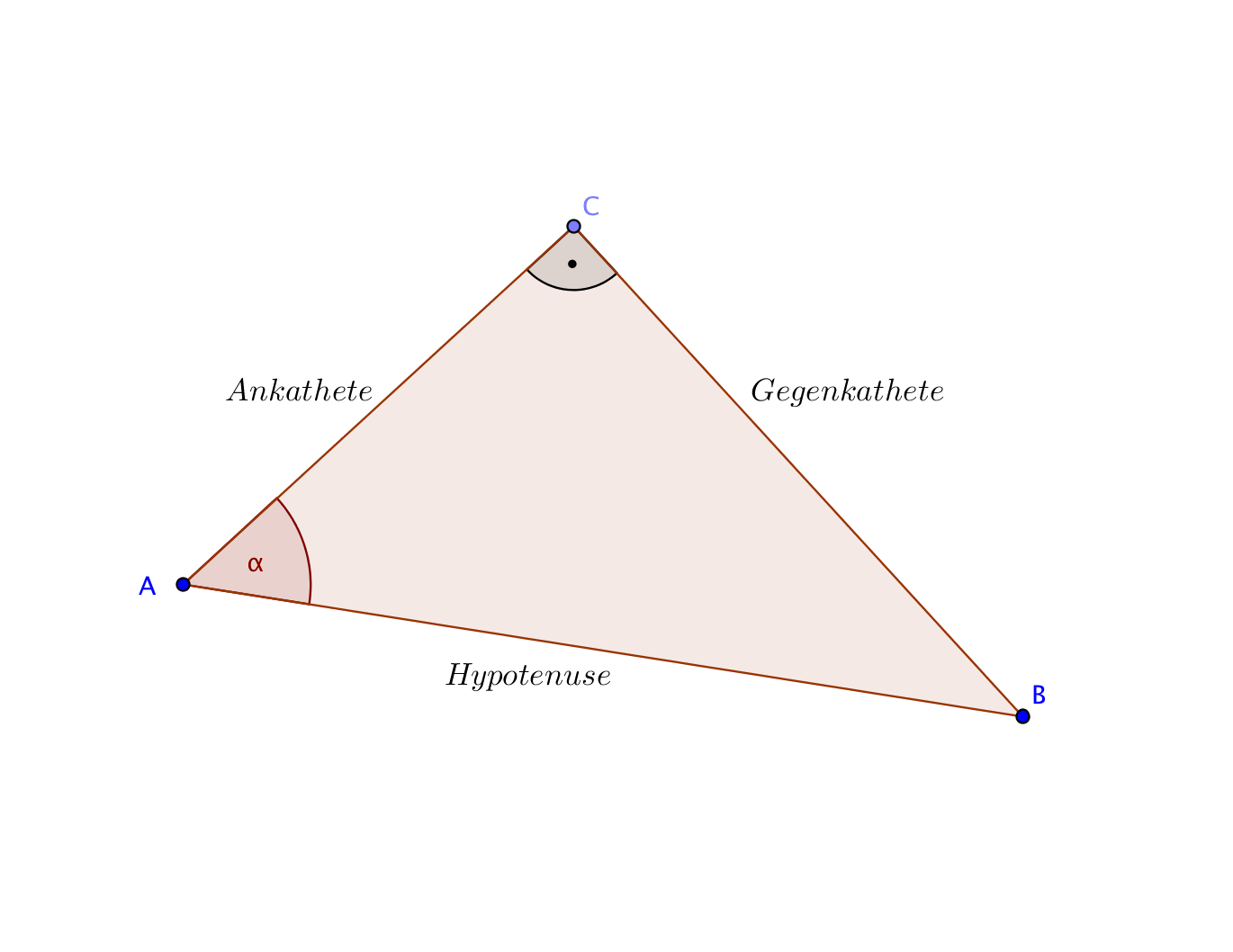
Auf diese Weise sind Sinus und Kosinus definiert für Winkel zwischen $0°$ und $90°$. Allgemeiner kann man Sinus und Kosinus für beliebige Drehwinkel definieren. Dazu betrachtet man den Einheitskreis in einem rechtwinkligen Koordinatensystem. Der Strahl im Winkel $\alpha$ zur positiven $x$-Achse trifft den Einheitskreis einem eindeutig bestimmten Punkt. Dieser Punkt hat die Koordinaten $$(\cos\alpha,\sin\alpha).$$ 
Bemerkung. Aus der allgemeineren Definition folgt sofort die Identität $$\sin\alpha=\sin(180°-\alpha).$$ Aus dem Peripheriewinkelsatz folgt damit: Ist $\overline{AB}$ eine Sehne in einem Kreis $\mathcal{K}$ und $C \in \mathcal{K}\setminus \{A,B\}$ ein Punkt, so ist $\sin\left(\sphericalangle ACB\right)$ unabhängig vom gewählten Punkt $C$.
Sinussatz, erste Version 7.4. Es sei $ABC$ ein Dreieck, $d$ der Durchmesser seines Umkreises, und $c = |AB|$. Dann gilt
$$
\sin \left(\angle ACB\right) = \frac{c}d.
$$
Beweis. Es sei $\overline{BC'}$ der Kreisdurchmesser des Umkreises. Nach dem Peripheriewinkelsatz 4.9 gilt $$\sin\left(\angle ACB\right)=\sin\left(\angle AC'B\right).$$ Andererseits ist $ABC'$ ein rechtwinkliges Dreieck mit $\overline{BC'}$ als Hypotenuse und $\overline{AB}$ als Gegenkathete zum Winkel $\angle AC'B$. Wegen der obigen Bemerkung und der Definition des Sinus gilt $$
\sin \left(\angle ACB\right) =\sin \left(\angle AC'B\right)= \frac{|AB|}{|BC'|}= \frac{c}d.
$$qed.
Sinussatz, zweite Version 7.5. Es sei $ABC$ ein Dreieck, $a$, $b$ und $c$ die Seiten $\overline{BC}$, $\overline{CA}$ und $\overline{AB}$, sowie $\alpha$, $\beta$ und $\gamma$ die Winkel an den Ecken $A$, $B$, und $C$. Dann gilt
$$
\frac{\sin \alpha}{\sin\beta} = \frac{a}{b},\;\; \frac{\sin \alpha}{\sin\gamma} = \frac{a}{c},\;\; \frac{\sin \beta}{\sin\gamma} = \frac{b}{c}.
$$
Beweis. Aus dem Sinussatz in der ersten Fromulierung erhalten wir mit dem Durchmesser $d$ des Umkreises die Gleichungen $\sin\alpha=\frac{a}d$ und $\sin\beta=\frac{b}d$. Somit gilt $$\frac{\sin\alpha}{\sin\beta}=\frac{\frac{a}d}{\frac{b}d}=\frac{a}b.$$ Die beiden anderen Gleichungen folgen auf analoge Weise.
qed.
Satz vom Apolloniuskreis 7.6. Es sei $\overline{AB}$ eine Strecke und $C$ ein Punkt der Strecke, der von den Punkten $A$ und $B$ verschieden ist und der nicht der Mittelpunkt der Strecke ist. Die Menge aller Punkte $S$, so dass $SC$ die Winkelhalbierende des Winkels $\angle ASB$ ist, ist ein Kreis. Er heisst Apolloniuskreis des Teilungspunktes $C \in
AB$.
Beweis. Es sei $D$ der Punkt der Geraden $AB$, für den die Punktepaare $AB$ und $CD$ harmonisch liegen. Ist $S$ ein Punkt in der Ebene, für welchen $SC$ die Winkelhalbierende des Winkels $\angle ASB$ ist, so liegt $S$ nach dem Lemma des Appolonius 5.12 auf dem Thaleskreis über $\overline{CD}$.
qed.
Anders formuliert, geht der Apolloniuskreis durch $C$ und hat seinen Mittelpunkt auf der Geraden $AB$. Ist $D$ der zweite Schnittpunkt von $AB$ mit dem Apolloniuskreis, so liegen die Punkte $A,B$ und $C,D$ harmonisch.
Korollar 7.6. Es sei $\lambda > 0$, $\lambda \neq 1$ eine reelle Zahl und $\overline{AB}$ eine Strecke. Die Menge aller Punkte $S$, für die gilt
$$
|SA| = \lambda |SB|,
$$ ist ein Kreis, dessen Mittelpunkt auf der Geraden $AB$ liegt. Bezeichnen $C,D$ die Schnittpunkte des Kreises mit der Geraden $AB$, so liegen die Punkte $A,B$ und $C,D$ harmonisch.
Beweis. Es sei $C$ der Punkt auf der Strecke $\overline{AB}$, für den gilt $$\lambda=\frac{|CA|}{|CB|}=\frac{|SA|}{|SB|}.$$ Dann ist die gesuchte Menge der Apolloniuskreis zum Punkte $C$.
qed.