Definition. Es seien $A,B$ und $C,D$ zwei Paare verschiedener Punkte auf einer Geraden. Das Doppelverhältnis der zwei Paare ist die reelle Zahl
$$
[A,B,C,D] =
\frac{\overset{\longrightarrow}{CA}}{\overset{\longrightarrow}{CB}} :
\frac{\overset{\longrightarrow}{DA}}{\overset{\longrightarrow}{DB}}
$$
Das Doppelverhältnis ist das Verhältnis von zwei Teilverhältnissen. Die Zahlen $0$ und $1$ können nicht als Doppelverhältnisse von Paaren verschiedener Punkte auftreten. Die Punktepaare liegen genau dann harmonisch, wenn gilt $$ [A,B,C,D] = -1.$$
Bemerkung. Gilt für jeweils verschiedene Punkte auf einer Geraden die Gleichung $$[A,B,C,D] =[A,B,C,D'],$$ so folgt auch $D=D'$. Denn in der Gleichung von Doppelverhältnissen kürzt sich ein Teilverhältnis und es folgt die Gleichung $$ \frac{\overset{\longrightarrow}{DA}}{\overset{\longrightarrow}{DB}}= \frac{\overset{\longrightarrow}{D'A}}{\overset{\longrightarrow}{D'B}}$$ und daraus folgt, wie wir bereits mehrfach benutzten, die behauptete Gleichung $D=D'$.
Proposition 5.14. In der Ebene seien zwei Geraden $g$ und $g'$ gegeben, sowie ein Punkt $Z$, der auf keiner der beiden Geraden liegt. Die Zentralprojektion mit Zentrum $Z$ bilde vier verschiedene Punkte $A,B,C,D$ in $g\setminus\{V\}$ auf die Punkte $A',B', C', D'$ in $g'\setminus\{F\}$ ab. Dann gilt:
$$
[A,B,C,D] = [A',B',C',D']
$$
Beweis. Sind $g$ und $g'$ parallel, so ist die Zentralprojektion laut dem dritten Strahlensatz affin. Teilverhältnisse ändern sich nicht durch affine Abbildungen und folglich auch nicht Doppelverhältnisse.
Sind $g$ und $g'$ nicht parallel, so betrachten wir die Parallele $g''$ zu $g'$ durch den Punkt $A$. Da $A$ nicht der Verschwindungspunkt $V$ ist, liegt $Z$ nicht auf der Geraden $g''$.
Zentralprojektion an $Z$ bildet die Punkte $A, B,C,D$ und $A',B',C',D'$ jeweils auf dieselben Punkt $A'',B'',C'',D''$ auf $g''$ ab. Der Punkt $B''$, zum Beispiel, ist der Schnittpunkt der Geraden $BB'$ mit $g''$. Es gilt $A=A''$. Da die Zentralprojektion an parallelen Geraden affin ist, gilt insbesondere $$
[A'',B'',C'',D''] = [A',B',C',D'].
$$ Wendet man den Satz des Menelaos zweimal auf das Dreieck $ABB''$ an, so ergibt sich für die Gerade $ZC$ die Gleichung $$
\frac{\overrightarrow{ZB''}}{\overrightarrow{ZB}}
\frac{\overrightarrow{C''A''}}{\overrightarrow{C''B''}}
\frac{\overrightarrow{CB}}{\overrightarrow{CA}}
= 1.
$$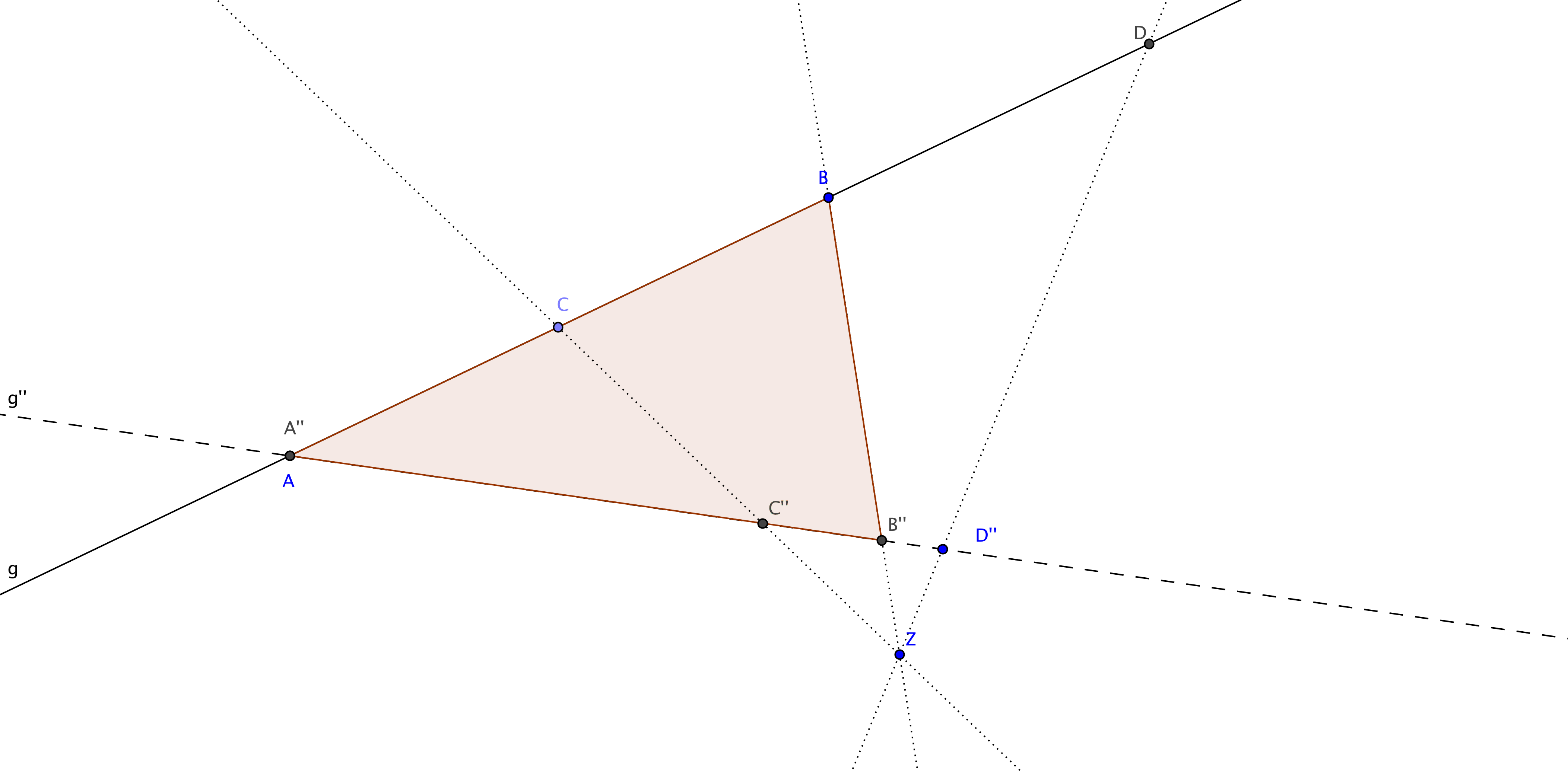
Für die Gerade $ZD$ ergibt sich
$$
\frac{\overrightarrow{ZB''}}{\overrightarrow{ZB}}
\frac{\overrightarrow{D''A''}}{\overrightarrow{D''B''}}
\frac{\overrightarrow{DB}}{\overrightarrow{DA}}
= 1.
$$ Nach Gleichsetzen und Kürzen des ersten Faktors erhalten wir daraus die Gleichung: $$
\frac{\overrightarrow{C''A''}}{\overrightarrow{C''B''}}
\frac{\overrightarrow{CB}}{\overrightarrow{CA}} =
\frac{\overrightarrow{D''A''}}{\overrightarrow{D''B''}}
\frac{\overrightarrow{DB}}{\overrightarrow{DA}}.
$$ Daraus folgt unmittelbar die zu beweisende Gleichung $$
[A'',B'',C'',D''] = [A,B,C,D].
$$qed.
Definition. Es seien $h_1$, $h_2$, $h_3$, $h_4$ vier verschiedene Geraden in der Ebene gegeben, die durch einen Punkt $Z$ gehen. Es sei $g$ eine Gerade in der Ebene, die weder durch $Z$ geht noch parallel zu einer der Geraden $h_i$ ist für $i = 1,2,3,4$. Sind $A_i = g \cap h_i$ die vier verschiedenen Schnittpunkte von $g$ mit den Geraden $h_i$, so wird das Doppelverhältnis $[h_1,h_2,h_3,h_4]$ der vier Geraden definiert durch die Gleichung
$$
[h_1,h_2,h_3,h_4] = [A_1,A_2,A_3,A_4].
$$
Der obige Satz (5.14) über die Zentralprojektion besagt, dass das derart definierte Doppelverhältnis der vier Geraden unabhängig von der Wahl der Testgeraden $g$ ist.
Satz und Definition 5.15. Es seien $A,B$ und $C,D$ vier verschiedene Punkte auf einem Kreis $K$. Das Doppelverhältnis $ [A,B,C,D]_K$ dieser Punkte ist definiert als das Doppelverhältnis $$
[A,B,C,D]_K:= [AP, BP, CP, DP]
$$ der Geraden $AP$, $BP$ und $CP$, $DP$ durch einen Punkt $P\in K\setminus \{A,B,C,D\}$. Diese Zahl ist unabhängig von der Wahl des Testpunktes $P$.
Beweis. Je zwei sich schneidenden Geraden $g$ und $g'$ kann man eindeutig einen Winkel zwischen $0°\lt \angle (g,g')\le 90°$ zuordnen. Das Doppelverhältnis vier sich schneidender Geraden hängt nur von den Winkeln zwischen den jeweiligen Geraden ab. Der Satz über den Peripheriewinkel (4.9) sagt aus, dass die Winkel zwischen den vier Geraden $AP$, $BP$ und $CP$, $DP$ unabhängig ist von der Wahl des Punktes $P$ auf dem Kreis.
qed.
Satz von Pascal 5.16. Es sei ein Kreis in der Ebene gegeben, sowie je drei Geraden in zwei Farben, sagen wir rot und grün. Es gelte, dass die roten Geraden den Kreis in denselben 6 Punkten schneiden, wie auch die grünen. Dann liegen die nicht auf dem Kreis liegenden Schnittpunkte roter und grüner Geraden auf einer Geraden.
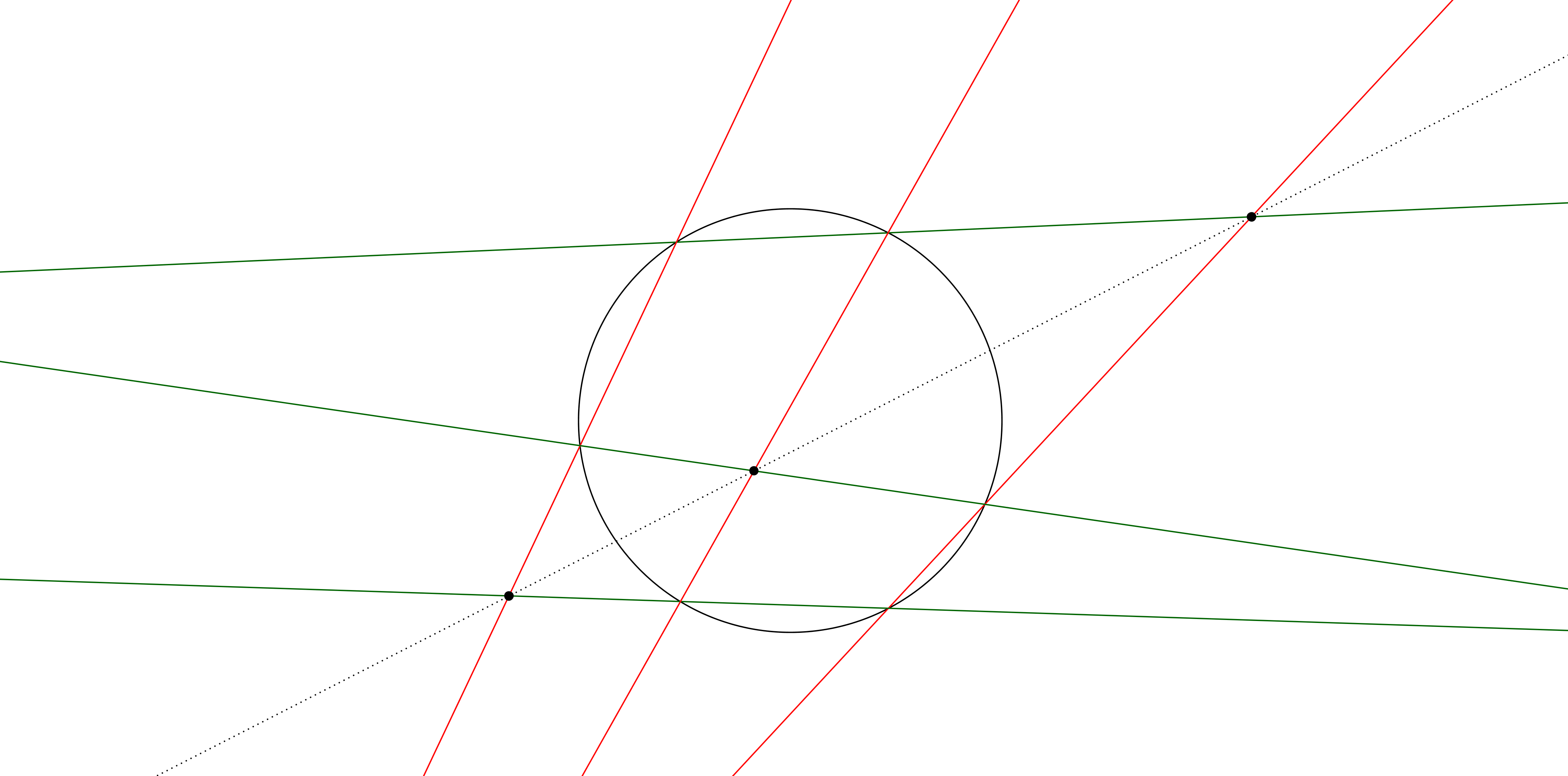
Beweis. Wir benennen die sechs Schnittpunkte der Geraden mit dem Kreis mit $A_0,A_1,\ldots, A_5$, so dass $A_0A_1$, $A_2A_3$ und $A_4,A_5$ die roten Geraden sind und $A_1A_2$, $A_3A_4$ und $A_5A_0$ die grünen. Wir projizieren die 4 Punkte $A_0,A_1,A_2,A_4$ zentral zum einen von $A_3$ auf die Gerade $A_0A_1$ und zum anderen von $A_5$ auf die Gerade $A_1A_2$.
Unter der Zentralprojektion mit Zentrum $A_3$ werden diese vier Punkte der Reihe nach auf $A_0, A_1$, $B_{45}$, $B_{25}$ abgebildet, unter der Zentralprojektion mit Zentrum $A_5$ auf $B_{34},A_1,A_2,B_{03}$. Es folgt für die Doppelverhältnisse:
$$[A_0,A_1,A_2,A_4]_K = [A_0,A_1,B_{45},B_{25}]=[B_{34},A_1,A_2,B_{03}].$$ Die Zentralprojektion $p$ mit Zentrum $B_{14}$ von der Geraden $A_0A_1$ auf die Gerade $A_1A_2$ bildet $A_0$ auf $B_{34}$ ab und $B_{45}$ auf $A_2$. Es gilt also die Gleichung
$$[B_{34},A_1,A_2,p(B_{25})] = [B_{34},A_1,A_2,B_{03}]$$ und folglich $p(B_{25})=B_{03}$. Da $p$ Projektion mit Zentrum $B_{14}$ ist, liegen $B_{03},B_{14},B_{25}$ auf einer Geraden.
qed.
Satz 5.17. Es sei $H$ der Höhenschnittpunkt eines Dreiecks $ABC$, $A'$ der Spiegelpunkt von $H$ an der Geraden $BC$. Dann liegt $A'$ auf dem Umkreis von $ABC$.
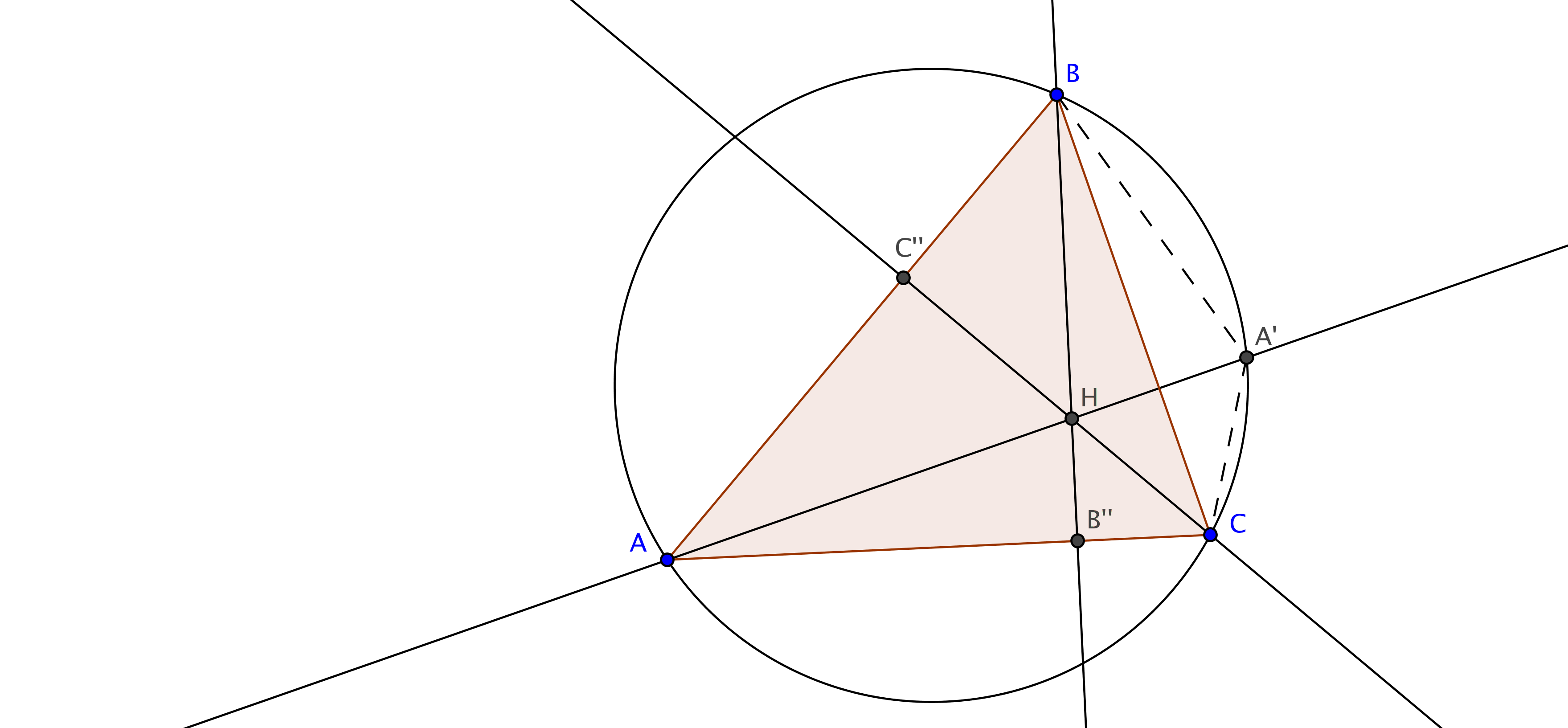
Beweis. Es seien $C''\in AB$ und $B''\in AC$ die Fußpunkte der Höhen durch $C$ und $B$. Die rechtwinkligen Dreiecke $ABB''$ und $HBC''$ sind ähnlich, da sie einen gemeinsamen Winkel bei $B$ haben. Insbesondere gilt $\angle CAB=\angle BHC''$ und damit $$\angle BHC=180°-\angle BAC.$$ Spiegelt man das Dreieck $BHC$ an der Geraden $BC$, so erhält man das Dreieck $BA'C$. Die Winkel $\angle BAC$ und $\angle BA'C$ ergänzen sich zu $180°$. Nach Satz (4.10) ist das Viereck $ABA'C$ ein Kreisviereck. Folglich liegt $A'$ auf dem Umkreis.
qed.
Satz von Steiner und Simpson 5.18. Es sei $ABC$ ein Dreieck und $P$ ein Punkt auf dem Umkreis. Es sei seien $P_A$, $P_B$ und $P_C$ die Bilder von $P$ unter den Spiegelungen an den Seiten $BC$, $CA$ und $AB$. Dann liegen die Punkte $P_A$, $P_B$ und $P_C$ auf einer Geraden.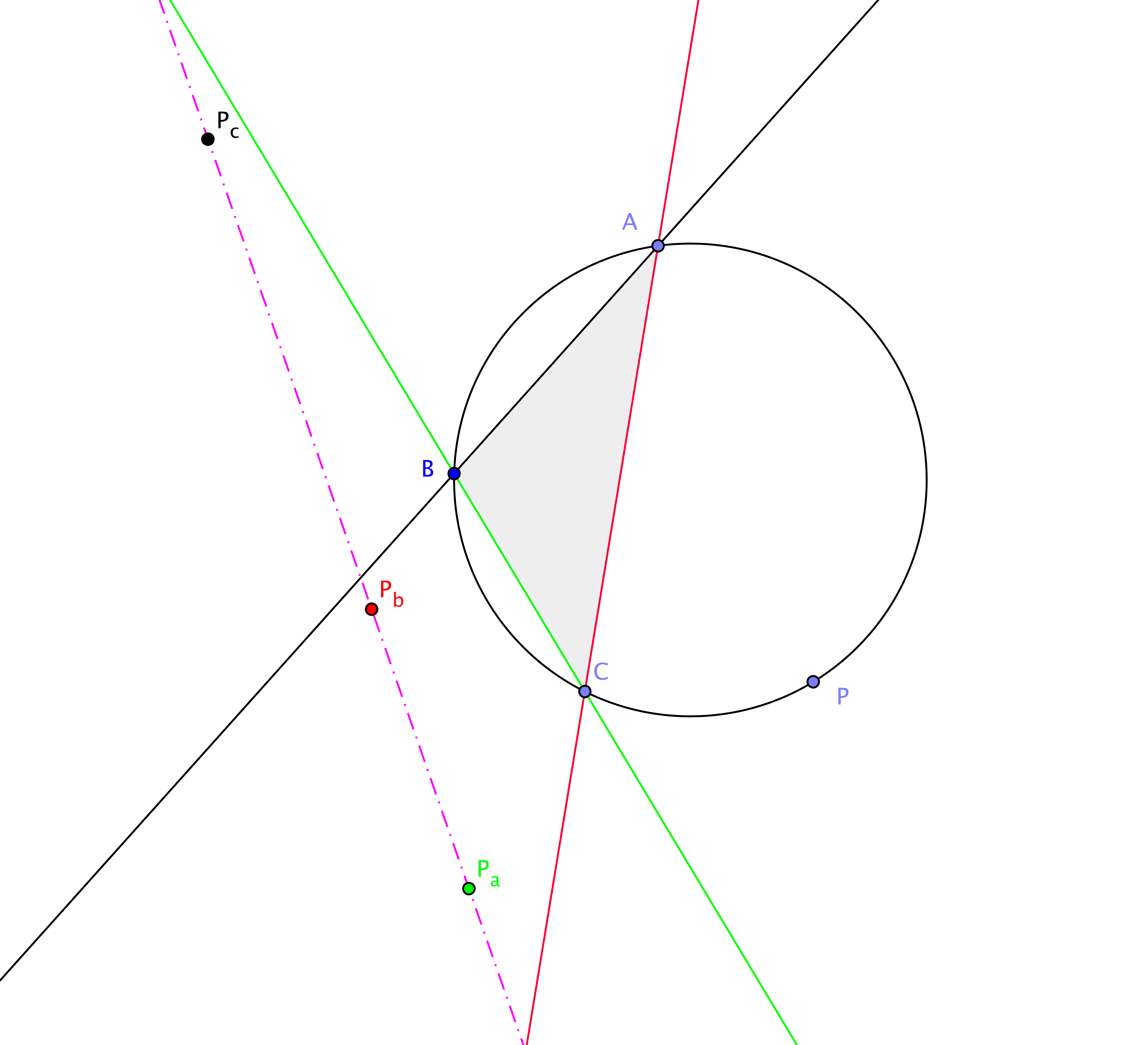
Beweis. Es seien $A'$ und $B'$ die Schnittpunkte des Umkreises mit den Höhen des Dreiecks durch die Punkte $A$ und $B$. Wir wenden den Satz von Pascal auf die grünen Geraden $AA'$, $PB'$ und $BC$, sowie die roten Geraden $A'P$, $B'B$ und $CA$ an.
Die Punkte
$$
D_b = AC \cap B'P , \quad D_a = CB \cap PA', \quad H = BB' \cap A'A .
$$ liegen auf einer Geraden $p=HD_a=HD_b$. Der Punkt $H$ ist der Höhenschnittpunkt des Dreiecks $ABC$.
Wir spiegeln jetzt die Gerade $A'P=A'D_a$ an der Seite $BC$. Der Punkt $A'$ wird nach Satz (5.17) in den Punkt $H$ gespiegelt und der Punkt $D_a$ bleibt fest. Also wird die Gerade $A'P$ in die Gerade $p$ gespiegelt. Insbesondere liegt der gespiegelte Punkt $P_A$ von $P$ auf der Geraden $p$.
Als Nächstes spiegeln wir die Gerade $B'P=B'D_b$ an der Seite $AC$. Der Punkt $B'$ wird nach Satz (5.17) in den Punkt $H$ gespiegelt und der Punkt $D_b$ bleibt fest. Also wird auch die Gerade $B'P$ in die Gerade $p$ gespiegelt und folglich liegt $P_B$ auf der Geraden $p$.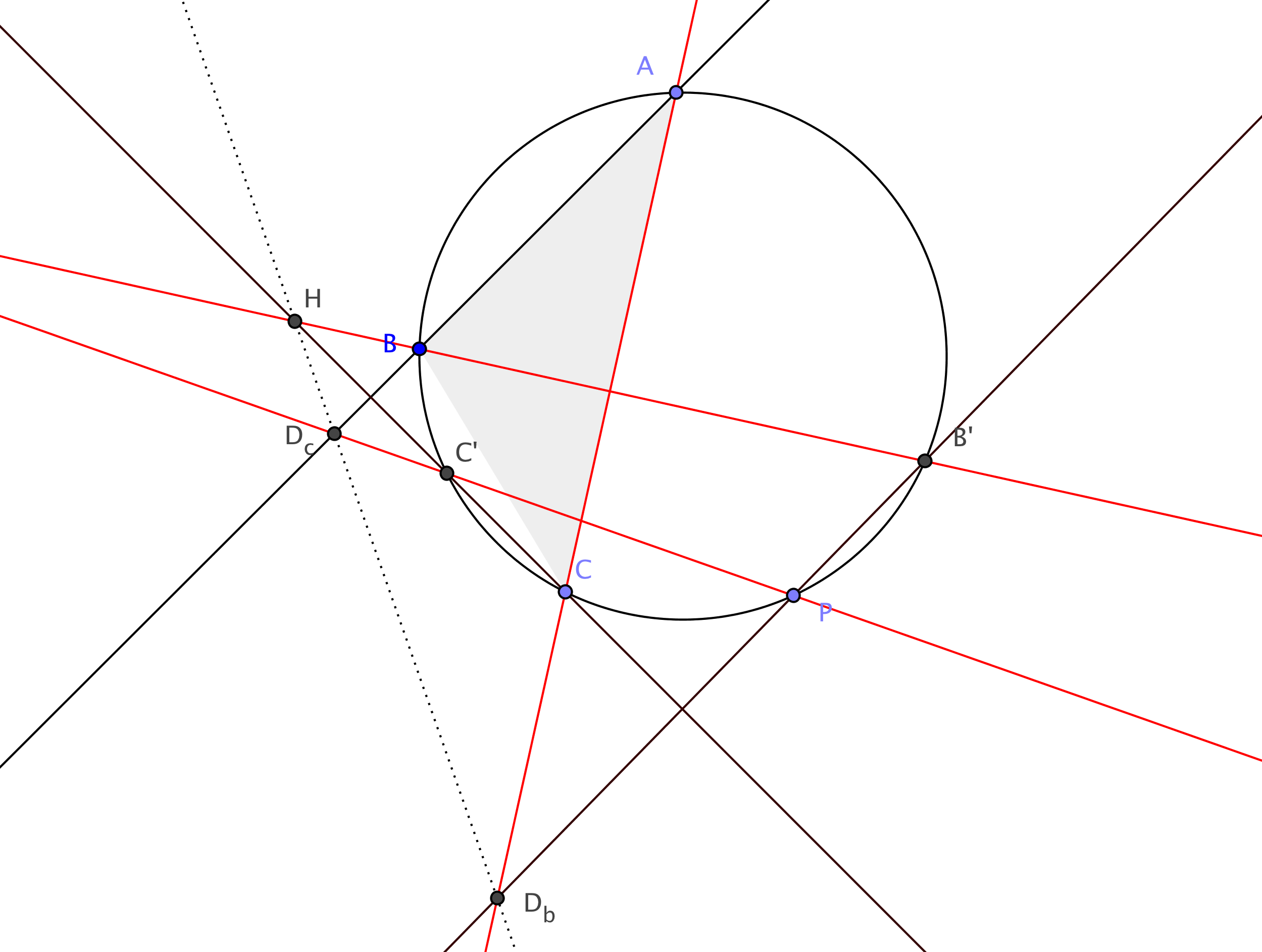
Wir vertauschen nun im obigen Argument die Rollen der Punkte $A,B,C$ in zyklischer Weise. Das heisst, wir wenden den Satz von Pascal auf die schwarzen Geraden $BA$, $CC'$ und $PB'$, sowie die roten Geraden $AC$, $C'P$ und $B'B$ an. Die Punkte $$
D_c = BA \cap C'P , \quad D_b = AC \cap PB', \quad H = CC' \cap B'B .
$$ liegen auf der Geraden $p=HD_b=HD_c$. Spiegeln wir die Gerade $C'P=C'D_c$ an der Seite $AB$, so wird $A'$ in den Punkt $H$ gespiegelt und $D_c$ bleibt fest. Also wird die Gerade $C'P$ in die Gerade $p$ gespiegelt und folglich liegt der Spiegelpunkt $P_C$ von $P$ auf der Geraden $p$.
qed.
Im obigen Beweis haben wir gleichzeitig auch folgende Aussage mitbewiesen:
Korollar 5.19. Für ein Dreieck $ABC$ seien $A',B',C'$ die Schnittpunkte des Umkreises mit den Höhen durch die Punkte $A$, $B$ und $C$. Es sei $P$ ein Punkt des Umkreises und $D_a = PA' \cap BC$, $D_b = PB' \cap AC$ und $D_c = PC' \cap AB$. Dann liegen die Punkte $D_a,D_b$ und $D_c$ auf einer Geraden.