Anders als die Parallelprojektion ist die Zentralprojektion im allgemeinen nicht affin. Um sie zu definieren, betrachten wir zwei Geraden $g$ und $g'$, sowie einen Punkt $Z$, der auf keiner der beiden Geraden liegt. Sind $g$ und $g'$ nicht parallel, so bezeichne $V$ den Schnittpunkt von $g$ mit der Parallelen zu $g'$ durch den Punkt $Z$ und $F$ den Schnittpunkt von $g'$ mit der Parallelen zu $g$ durch den Punkt $Z$.
Definition. Die Zentralprojektion mit Zentrum $Z$ ist eine Abbildung $p: g\setminus\{V\}\to g' \setminus\{F\}$, die einem Punkt $A \in g\setminus \{V\}$ den Schnittpunkt $p(A)$ der Geraden $AZ$ mit $g'$ zuordnet. Man nennt $Z$ auch den Augpunkt und die Geraden durch $Z$ Sehstrahlen. Der Punkt $V$ heisst dann Verschwindungspunkt und $F$ Fluchtpunkt. Sind $g$ und $g'$ parallel, so gibt es weder Verschwindungspunkt noch Fluchtpunkt. Die durch die Abbildungsvorschrift beschriebene Zentralprojektion ist dann eine auf allen Punkten von $g$ definierte Abbildung $p:g\to g'$.
Die Bezeichnung $g\setminus \{V\}$ steht für die mengentheoretische Differenz. Man sagt $g$ ohne $V$.
Dritter Strahlensatz 5.6. Es seien $g$ und $g'$ parallele Geraden und $Z$ ein Punkt, der zu keiner der Geraden gehört. Dann ist die Zentralprojektion $p: g \rightarrow g'$ mit Zentrum $Z$ affin.
Beweis. Es seien $A,B,C$ verschiedene Punkte in $g$ und $A',B',C'$ die Bildpunkte unter der Zentralprojektion.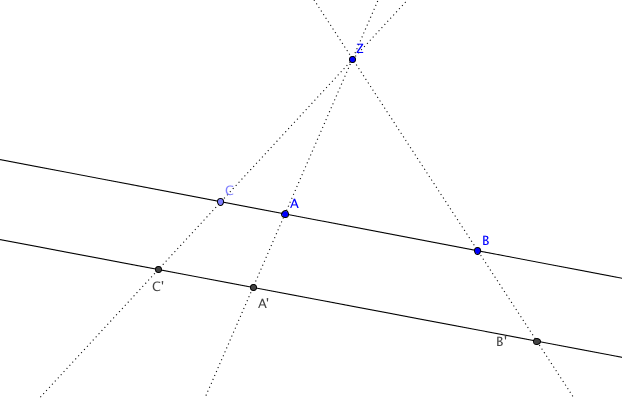
Nach dem zweiten Strahlensatz gilt $$
\frac{\overrightarrow{AB}}{\overrightarrow{A'B'}}
= \frac{\overrightarrow{ZA}}{\overrightarrow{ZA'}}
= \frac{\overrightarrow{AC}}{\overrightarrow{A'C'}} .
$$ Es folgt die Gleichung $$
\frac{\overrightarrow{AB}}{\overrightarrow{AC}}
= \frac{\overrightarrow{A'B'}}{\overrightarrow{A'C'}}
.$$ Denn die Vektoren $ \overset{\longrightarrow}{A'B'}$, $\overset{\longrightarrow}{AC}$ und $ \overset{\longrightarrow}{A'C'}$ sind allesamt Streckungen des Vektors $ \overset{\longrightarrow}{AB}$. Somit sind diese Teilverhältnisse definiert. Außerdem ist der Betrag der Teilverhältnisse gleich dem Quotienten der Längen der jeweiligen Strecken. Folglich gilt die Gleichung zumindest bis auf's Vorzeichen. Das Vorzeichen ist aber auch klar: Eine Zentralprojektion bildet in gleiche (bzw. entgegengesetzte) Richtung zeigende Vektoren auf in gleiche (bzw. entgegengesetzte) Richtung zeigende Vektoren ab.
qed.
Korollar 5.7. Es sei $ABCD$ ein echtes Trapez mit den parallelen Seiten $AB$ und $CD$. Es sei $Z$ der Schnittpunkt der Seiten $BC$ und $AD$ und es sei $T$ der Schnittpunkt der Diagonalen $AC$ und $BD$. Dann halbiert die Verbindungsgerade $ZT$ jeweils die Strecken $AB$ und $CD$.
Beweis. Wir betrachten die Zentralprojektion mit dem Zentrum $Z$ von der Geraden $AB$ auf die Gerade $CD$. Da die Abbildung affin ist, wird der Mittelpunkt der Strecke $\overline{AB}$ auf den Mittelpunkt von $\overline{CD}$ abbgebildet. Also liegt $Z$ auf der Gerade $m$, die den Mittelpunkt von $\overline{AB}$ mit dem Mittelpunkt von $\overline{CD}$ verbindet.
Betrachten wir die Zentralprojektion mit Zentrum $T$ von der Gerade $AB$ auf die Gerade $CD$, so sehen wir, dass auch $T$ auf $m$ liegt. Die Behauptung folgt.
qed.