Drei Punkte $A,B,C$ der Ebene bilden ein Dreieck $ABC$, bestehend aus den drei Strecken $c=\overline{AB},a=\overline{BC}$ und $a=\overline{CA}$. Liegen die drei Punkte auf einer Geraden, so nennen wir das Dreieck ausgeartet. Andernfalls bestimmen sie gemäß dem Prinzip (1.3) einen eindeutig bestimmten Kreis, der die drei Punkte enthält. Diesen Kreis nennt man Umkreis.
In einem Dreieck $ABC$ bezeichnen wir mit $$\sphericalangle ABC=\sphericalangle \left(\overset{\mapsto}{BC}, \overset{\mapsto}{BA}\right)$$ den Drehwinkel derjenigen Drehung, die den von $B$ in Richtung $A$ ausgehenden Strahl $\overset{\mapsto}{BA}$ in den von $B$ in Richtung $C$ ausgehenden Strahl $\overset{\mapsto}{BC}$ abbildet. Dies macht natürlich nur Sinn, wenn diese Strahlen definiert sind, d.h. wenn $A\not=B$ und $B\not= C$ gilt.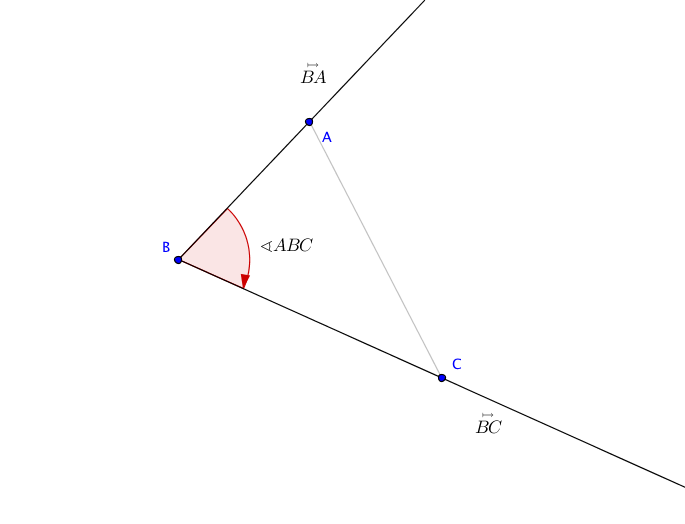
Zur Erinnerung: Der geometrische Winkel, den auch Euklid benutzt, bezeichnen wir mit $\angle ABC$. Es gilt $0°\le\angle ABC\le
180°$. Man setzt $$\angle ABC=\begin{cases}
\sphericalangle ABC & \text{ wenn } 0°\le\sphericalangle ABC\le 180°\\
360°-\sphericalangle ABC & \text{ wenn } 180°\le\sphericalangle ABC\le 360°
\end{cases}.$$ Mit dieser Konvention gilt $\angle ABC=\angle CBA$, aber $\sphericalangle ABC=-\sphericalangle CBA$.
Satz 3.1 Winkelsumme im Dreieck. Für drei je paarweise verschiedene Punkte $A,B,C$ der Ebene gilt:
$$\sphericalangle ABC+\sphericalangle BCA+\sphericalangle
CAB=180°.$$ Diese Formel bleibt richtig, wenn man Drehwinkel durch geometrische Winkel ersetzt.
Beweis. Wir benutzen die Summen- oder Kürzungsformel für Drehwinkel. Es gilt $$\begin{align*}
\sphericalangle ABC+\sphericalangle BCA+\sphericalangle CAB&= \sphericalangle \left(\overset{\mapsto}{BC}, \overset{\mapsto}{BA}\right)+\sphericalangle \left(\overset{\mapsto}{CA}, \overset{\mapsto}{CB}\right)+\sphericalangle \left(\overset{\mapsto}{AB}, \overset{\mapsto}{AC}\right)\\
&=\sphericalangle \left(\overset{\mapsto}{BC}, \overset{\mapsto}{BA}\right)+\sphericalangle \left(\overset{\mapsto}{AC}, \overset{\mapsto}{BC}\right)+\sphericalangle \left(\overset{\mapsto}{AB}, \overset{\mapsto}{AC}\right)\\
&=\sphericalangle \left(\overset{\mapsto}{AC}, \overset{\mapsto}{BA}\right)+\sphericalangle \left(\overset{\mapsto}{AB}, \overset{\mapsto}{AC}\right)\\
&=\sphericalangle \left(\overset{\mapsto}{AB}, \overset{\mapsto}{BA}\right)\\
&=180°\end{align*}$$ In dieser Gleichungskette passiert folgendes:
- In der ersten Gleichung schreiben wir nur die Definition des Drehwinkels zwischen je drei Punkten um in die Definition des Drehwinkels zwischen je zwei Strahlen.
- In der zweiten Gleichung benutzen wir die schon früher bemerkte Gleichheit der Wechselwinkel $\sphericalangle(s,t)=\sphericalangle(-s,-t)$ für zwei Strahlen $s$ und $t$. Wenn wir beide Strahlen jeweils durch ihr Negatives ersetzen, so erhalten wir den gleichen Drehwinkel.
- In den nächsten beiden Gleichungen benutzen wir die Kürzungsformel: Tritt ein Strahl in der Summe einmal im ersten und einmal im zweiten Eintrag eines Drehwinkels auf, so kann man die beiden Einträge kürzen. Hier betrifft das zuerst den Strahl $\overset{\mapsto}{BC}$ und dann den Strahl $\overset{\mapsto}{AC}$.
- Die letzte Gleichung besagt, dass zwei entgegengesetzt gerichtete Strahlen den Drehwinkel von $180°$ zueinander besitzen.
qed.