Definition. Zwei Dreiecke $ABC$ und $A'B'C'$ heißen kongruent, wenn es eine Isometrie $\sigma$ gibt mit $\sigma(A)=A'$, $\sigma(B)=B'$ und $\sigma(C)=C'$.
Isometrien erhalten Abstände und geometrische Winkel. Insbesondere sind für kongruente Dreiecke die folgenden sechs Gleichungen erfüllt: $$|AB|=|A'B'|,\quad |AC|=|A'C'|, \quad |BC|=|B'C'|$$$$\angle ABC=\angle A'B'C', \quad \angle BCA=\angle B'C'A',\quad \angle CAB=\angle C'A'B'.$$ Ist das Dreieck $ABC$ nicht ausgeartet, so beschreibt die Strecke $\overline{AB}$, zusammen mit der Angabe der Halbebene bezüglich der Geraden $AB$, in welcher der dritte Eckpunkt $C$ liegt, eine beseitete Strecke. Ebenso beschreibt die Lage des Punktes $C'$ bezüglich der Strecke $\overline{A'B'}$ eine beseitete Strecke. Sind die beiden Dreiecke $ABC$ und $A'B'C'$ kongruent, d.h. werden sie durch eine Isometrie $\sigma$ auf einander abgebildet, so bildet $\sigma$ insbesondere die beiden beseiteten Strecken aufeinander ab. Wegen Satz (2.17) ist die Isometrie $\sigma$ dann eindeutig bestimmt.
Die oben angeführten sechs Gleichungen sind redundant: Um festzustellen, ob zwei gegebene Dreiecke tatsächlich kongruent sind, ist es nicht nötig, alle diese sechs Daten, nämlich die drei Seitenlängen und die drei Winkel, zu vergleichen. In manchen Fällen reichen drei dieser sechs Daten aus. Die Kongruenzsätze sagen, welche Datensätze Dreiecke bis auf Kongruenz eindeutig identifizieren.
Kongruenzsatz SSS 3.2. Es seien $ABC$ und $A'B'C'$ zwei nicht ausgeartete Dreiecke mit gleichen Seitenlängen. Es gelten also die Gleichungen $|AB|=|A'B'|$, $ |AC|=|A'C'|$ $|BC|=|B'C'|$. Dann sind die beiden Dreiecke kongruent.
Beweis. Nach Voraussetzung sind die beiden Strecken $\overline{AB}$ und $\overline{A'B'}$ gleich lang. Gemäß Satz (2.1) gibt es genau zwei Isometrieen $\sigma$ und $\sigma'$ , die $A$ in $A'$ und $B$ in $B'$ überführen. Bezeichnen wir die Gerade $AB$ mit $g$, so gilt $\sigma'=s_g\circ \sigma$. Wir müssen zeigen, dass eine dieser beiden Isometrien den Punkt $C$ in $C'$ abbildet.
Der Punkt $C$ liegt auf dem Kreis mit Radius $|BC|$ und Mittelpunkt $B$ und auf dem Kreis mit Radius $|AC|$ um den Punkt $A$. Beide Isometrien bilden die zwei Kreise um $B$ und $A$ ab auf die Kreise mit Radius $|B'C'|=|BC|$ und Mittelpunkt $B'$ und mit Radius $|A'C'|=|AC|$ um den Punkt $A'$. Die Punkte $C'$ und $s_g(C')$ sind die Schnittpunkte dieser beiden Kreise. Der Punkt $C$ wird also durch $\sigma$ auf einen dieser beiden Punkte $C'$ oder $s_g(C')$ abgebildet, durch $s_g\circ\sigma$ auf den anderen. Eine der beiden Isometrien bildet jedenfalls den Punkt $C$ in $C'$ ab. Das war zu zeigen.
qed.
Der Kongruenzsatz SSS gilt ebenso für ausgeartete Dreiecke.
Kongruenzsatz WSW 3.3. Es seien $ABC$ und $A'B'C'$ zwei nicht ausgeartete Dreiecke, so dass $|AB|=|A'B'|$ und $\angle CAB= \angle C'A'B'$ und $\angle CBA = \angle C'B'A'$. Dann sind die beiden Dreiecke kongruent.
Beweis. Nach Voraussetzung sind die beiden Strecken $\overline{AB}$ und $\overline{A'B'}$ gleich lang. Gemäß Satz (2.1) gibt es genau eine Isometrie $\sigma$, die $A$ in $A'$ und $B$ in $B'$ überführt und die Halbebene bezüglich der Geraden $AB$, in welcher der Punkt $C$ liegt, in die Halbebene bezüglich der Geraden $A'B'$, in welcher der Punkt $C'$ liegt, abbildet. Wir müssen zeigen, dass $\sigma$ den Punkt $C$ in $C'$ abbildet.
Der Punkt $C$ liegt auf den beiden Strahlen, die mit Winkel $\angle BAC$ der von $A$ und mit Winkel $\angle ABC$ von $B$ aus in die durch den Punkt $C$ bestimmte Halbebene ragen. Die beiden Strahlen werden durch $\sigma$ in Strahlen abgebildet, welche mit Winkel $\angle B'A'C'$ von $A'$ aus und mit Winkel $\angle A'B'C'$ von $B'$ aus in die durch den Punkt $C'$ bestimmte Halbebene ragen. Dies gilt, da jede Isometrie geometrische Winkel erhält. Der Schnittpunkt $C$ der beiden Strahlen im Urbild wird in den Schnittpunkt $C'$ der beiden Bildstrahlen abgebildet. Das war zu zeigen.
qed.
Im Falle von ausgearteten Dreiecken ist der Kongruenzsatz WSW nicht gültig, denn die beiden Halbstrahlen liegen auf der Geraden $AB$ und haben mehr als nur einen Schnittpunkt.
Kongruenzsatz SWS 3.4. Es seien $ABC$ und $A'B'C'$ zwei nicht ausgeartete Dreiecke, so dass $|AB|=|A'B'|,\; |CB|=|C'B'|$ und $\angle ABC= \angle A'B'C'$. Dann sind die beiden Dreiecke kongruent.
Beweis. Nach Voraussetzung sind die beiden Strecken $\overline{AB}$ und $\overline{A'B'}$ gleich lang. Gemäß Satz (2.1) gibt es genau eine Isometrie $\sigma$, die $A$ in $A'$ und $B$ in $B'$ überführt und die Halbebene bezüglich der Geraden $AB$, in welcher der Punkt $C$ liegt, in die Halbebene bezüglich der Geraden $A'B'$, in welcher der Punkt $C'$ liegt, abbildet. Wir müssen zeigen, dass $\sigma$ den Punkt $C$ in $C'$ abbildet.
Der Punkt $C$ ist der eindeutig bestimmte Schnittpunkt des Strahls, der mit Winkel $\angle ABC$ von $B$ aus in die durch den Punkt $C$ bestimmte Halbebene ragt, sowie des Kreises mit Radius $|BC|$ um den Punkt $B$. Der Strahl wird durch $\sigma$ in den Strahl abgebildet, welcher mit Winkel $\angle A'B'C'$ von $B'$ aus in die durch den Punkt $C'$ bestimmte Halbebene ragt. Dies gilt, da jede Isometrie geometrische Winkel erhält. Der Kreis wird auf den Kreis mit Radius $|B'C'|$ um $B'$ abgebildet. Der Schnittpunkt $C$ von Strahl und Kreis im Urbild wird in den Schnittpunkt $C'$ von Bildstrahl und Bildkreis abgebildet. Das war zu zeigen.
qed.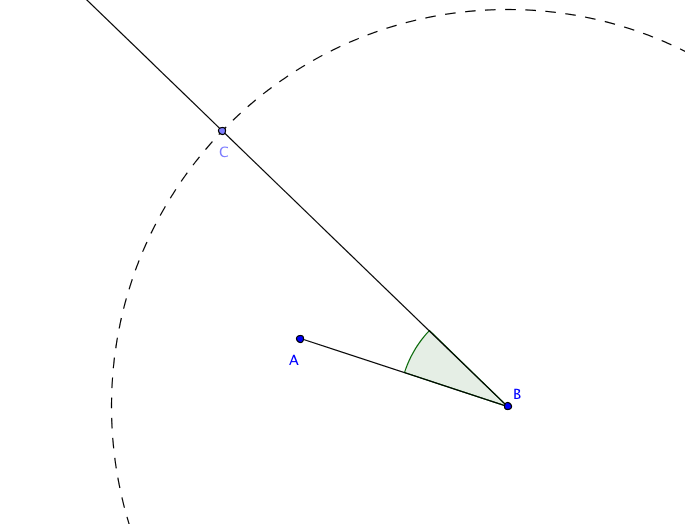
Der Kongruenzsatz SWS gilt ebenso für ausgeartete Dreiecke, solange nur der Winkel definiert ist, das heißt, es muss gelten $A\not= B\not=C$.
Zwei Dreiecke $ABC$ und $A'B'C'$, mit $|AB|=|A'B'|,\; |CB|=|C'B'|$ und $\angle ABC= \angle A'B'C'$ müssen nicht notwendig kongruent sein. Das heißt, einen allgemein gültigen Kongruenzsatz SSW gibt es nicht. In der Graphik zum Beispiel erfüllen die offensichtlich nicht kongruenten Dreiecke $ABC$ und $A'B'C'$ mit $A=A'$ und $B=B'$ die geforderten Bedingungen.
Fordert man zusätzlich $|CB| > |AB|$, so ändert sich die Situation. In diesem Fall hat der von $A$ im vorgegebenen Winkel ausgehende Strahl statt zweier Schnittpunkte nur einen Schnittpunkt mit dem Kreis um $B$ im Radius $|BC|$. Der entsprechende Kongruenzsatz wird gelegentlich mit SsW abgekürzt, um anzuzeigen, dass der Winkel an der kürzeren Strecke anliegt.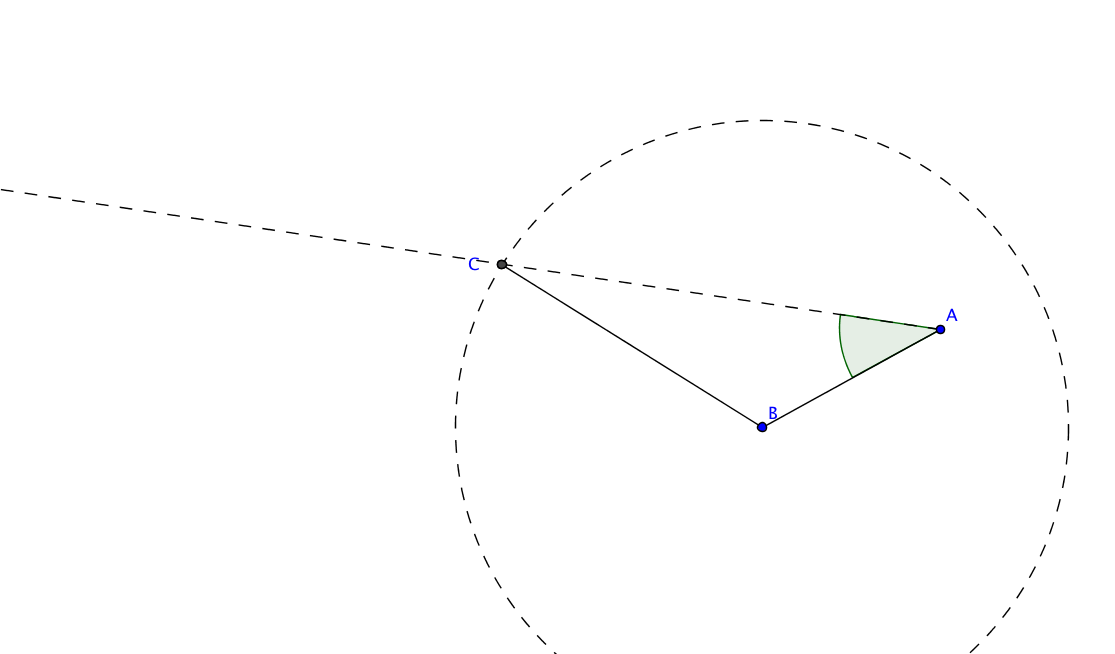
Wir formulieren einen Spezialfall dieses Kongruenzsatzes:
Korollar 3.5. Es seien $ABC$ und $A'B'C'$ zwei Dreiecke, so dass $|AB|=|A'B'|,\; |CB|=|C'B'|$ und $\angle CAB = 90^{o} = \angle C'A'B'$. Dann sind die beiden Dreiecke kongruent.
Beweis. Man spiegelt das Dreieck $ABC$ an der Geraden $AC$. Es sei $B_1$ das Spiegelbild von $B$. Nach Voraussetzung ist $A$ der Mittelpunkt der Strecke $B_1B$. Es gilt: $|BC| = |B_1C|$ und $|B_1B| =2|CB|$.
Mit dem Dreieck $A'B'C'$ verfahren wir in der gleichen Weise. Dann folgt aus dem Kongruenzsatz SSS, dass die beiden Dreiecke $ABB_1$ und $A'B'B'_1$ kongruent sind. Daraus erhalten wir die Behauptung.
qed.
Eselsbrücke 3.6. Es sei $ABC$ ein Dreieck. Wenn $\angle ABC=\angle BAC$, so gilt $|CA|=|CB|$. Wenn umgekehrt $|CA|=|CB|$ so gilt $\angle ABC=\angle BAC$.
Beweis. Wir betrachten das Dreieck auf zwei verschiedene Weisen. Einmal als Dreieck $ABC$ und einmal als Dreieck $A'B'C'$ mit $A'=B$, $B'=A$ und $C'=C$.
Angenommen, es gilt die Gleichheit der Winkel $\angle ABC=\angle BAC$. Dann gilt $|AB| = |BA|=|A'B'|$. Für die Winkel gilt $\angle ABC=\angle BAC=\angle A'B'C'$. Die erste Gleichung gilt nach Voraussetzung. Die zweite Gleichung nach unserer Definition der Punkte $A'$, $B'$ und $C'$. Analog gilt $\angle BAC=\angle ABC=\angle B'A'C'$. Der Kongruenzsatz WSW liefert uns nun, dass die beiden Dreiecke kongruent sind. Folglich gilt $|CA|=|C'A'|=|CB|$.
Angenommen, es gilt $|CA|=|CB|$. Das heißt, es gilt $|C'A'|=|CB|=|CA|$ und $|C'B'|=|CA|=|CB|$. Die Gleichheit $|AB|=|BA|=|A'B'|$ gilt ebenso. Folglich sind die beiden Dreiecke $ABC$ und $A'B'C'$ nach dem Kongruenzsatz SSS kongruent. Daraus folgt die Gleichheit der Winkel: $\angle CAB=\angle C'A'B'=\angle CBA$.
qed. 
Aus dem Beweis folgt für die Drehwinkel $\sphericalangle CAB= -
\sphericalangle CBA$.