Definition. Es seien $g$, $g'$ und $h$ Geraden in der Ebene. Wir nehmen an, die Gerade $h$ sei weder zu $g$ noch zu $g'$ parallel. Die Parallelprojektion $$f:g \rightarrow g'$$ mit Projektionsrichtung $h$ ist die Abbildung, die einem Punkt $A \in g$ den Schnittpunkt $f(A) = h_A \cap g'$ der Geraden $g'$ mit der Parallelen $h_A$ zu $h$ durch $A$ zuordnet.

Erster Strahlensatz 5.3. Die Parallelprojektion ist eine affine Abbildung.
Um diese Aussage zu verifizieren benutzen wir ein Koordinatensystem in der Ebene. Ein solches Koordinatensystem liefert uns ein algebraisches Modell der euklidischen Geometrie. Das Computerprogramm Geogebra, das wir zur Veranschaulichung heranziehen, benutzt im Hintergrund dieses algebraische Modell, um seine Graphiken zu berechnen. Es würde zu weit führen, dieses Modell in allen Einzelheiten zu besprechen. Die Anschaulichkeit der Geometrie würde sehr schnell unter einem Wust von Formeln verschwinden. Wir geben uns damit zufrieden, dass die Geometrie es ermöglicht, gewisse Arten von algebraischen Problemen anschaulich zu formulieren und ohne Rechnung elegant zu lösen. Was sich mühelos in einer Zeichnung mit einigen Kreisen und Geraden skizzieren lässt, ist algebraisch oft nur mit großem Aufwand nachzuvollziehen. Tatsächlich hilft die geometrische Anschauung bei algebraischen Problemen häufig, den richtigen Lösungsansatz zu entdecken.
Es sollen nur einige Grundkonzepte dieses algebraischen Modells der euklidischen Geometrie vorgestellt werden: Punkte, Geraden und Translationen, oder synonym Vektoren. Ein Punkt $$A=(a_1,a_2)$$ der Ebene wird in einem Koordinatensystem beschrieben durch ein geordnetes Paar reeller Zahlen $a_1,a_2\in \mathbb R$. Eine Translation $T$ der Ebene wird ebenfalls beschrieben durch ein Paar $$T=(t_1,t_2)$$ reeller Zahlen $t_1,t_2\in \mathbb R$. Die Translation wirkt dabei durch koordinatenweise Addition \begin{align*}T:\mathbb E&\longrightarrow\mathbb E\\A=(a_1,a_2)&\mapsto (a_1+t_1,a_2+t_2)=A+T.\end{align*} Verschiebt die Translation $T$ den Punkt $A=(a_1,a_2)$ in den Punkt $B=(b_1,b_2)$, so gilt $$T=\overset{\longrightarrow}{AB}=(b_1-a_1,b_2-a_2)=B-A,$$ denn es gilt $$A+\overset{\longrightarrow}{AB}=B=A+(B-A),$$ oder in Koordinaten ausgedrückt $$(a_1,a_2)+(b_1-a_1,b_2-a_2)=(b_1,b_2).$$ Die Streckung eines Vektors $T$ um den Faktor $\lambda\in \mathbb R$ wird in Koordinatenschreibweise beschrieben durch die Multiplikation beider Koordinaten mit $\lambda$, also $$\lambda\,T=\lambda(t_1,t_2)=\left(\lambda t_1,\lambda t_2\right).$$
Beweis von (5.3). Ist $g=g'$, so ist die Parallelenprojektion die identische Abbildung und es ist nichts zu zeigen. Wir nehmen also an $g\not= g'$. Es seien $A,B,C$ paarweise verschiedene Punkte auf der Geraden $g$ und $A',B',C'$ die jeweiligen Bilder unter der Parallelprojektion entlang $h$. Wir nehmen an, dass $B\not=B'$ gilt. Ansonsten muss gelten $C\not= C'$ und wir vertauschen im folgenden die Buchstaben $B$ und $C$. Es sei $$\lambda_C=\frac{\overrightarrow{AC}}{\overrightarrow{AB}}.$$
Zu beweisen ist $$\lambda_C\overset{!}=\frac{\overrightarrow{A'C'}}{\overrightarrow{A'B'}}.$$ Das heisst, der Punkt $A'+\lambda_C \overset{\longrightarrow}{A'B'}$ ist der Schnittpunkt $C'=h_C\cap g'$. Da der Punkt $A'+\lambda_C \overset{\longrightarrow}{A'B'}$ auf der Geraden $g'$ liegt, reicht es zu zeigen, dass er auch auf der Geraden $h_C$ liegt. Wir müssen also zeigen, dass der Differenzvektor $$\left(A'+\lambda_C\overset{\longrightarrow}{A'B'}\right) -C$$ eine Streckung des Vektors $\overset{\longrightarrow}{BB'}=B'-B$ ist. Dazu rechnen wir \begin{align*}
\left(A'+\lambda_C\overset{\longrightarrow}{A'B'}\right) -C&=\left(A'+\lambda_C\overset{\longrightarrow}{A'B'}\right) -\left(A+\lambda_C\overset{\longrightarrow}{AB}\right) \\
&=\left(A'+\lambda_C(B'-A')\right) -\left(A+\lambda_C(B-A)\right) \\
&=(1-\lambda_C)(A'-A)+\lambda_C(B'-B).\end{align*} Der Differenzvektor $A'-A$ ist eine Streckung des Vektors $B'-B$, also gibt es eine reelle Zahl $\nu$ mit $$A'-A=\nu(B'-B)$$ und wir können die Gleichungskette fortsetzen zu \begin{align*}
\left(A'+\lambda_C\overset{\longrightarrow}{A'B'}\right) -C&=\left(\nu-\lambda_C\nu+\lambda_C\right)(B'-B).\end{align*}qed.
Für Vektoren $T,S,R$ und Zahlen $\mu, \lambda \in \mathbb{R}$ gelten folgende Rechenregeln.
\begin{equation}
\begin{array}{rcl}
S + T & = & T + S\\
(R + S) + T & = & R + (S + T)\\
T + \overset{\rightarrow}{0} & = & T\\
0 \cdot T & = & \overset{\rightarrow}{0}\\
\lambda \overset{\rightarrow}{0} & = & \overset{\rightarrow}{0}\\
(\lambda + \mu)T & = & \lambda T + \mu T\\
\lambda(S + T) & = & \lambda S + \lambda T\\
\end{array}
\end{equation} Die letzte dieser Regeln ist tatsächlich äquivalent zum ersten Strahlensatzes.
Eine Anwendung. Es sei $ABC$ ein Dreieck und es sei $D_0$ ein Punkt auf der Seite $b=\overline{AC}$. Man laufe auf einer Parallelen zu der Seite $a=\overline{BC}$ durch $D_0$ bis man zu einem Punkt $D_1$ auf der Seite $c=\overline{AB}$ kommt. Genauso laufe man von $D_1$ parallel zu $b$ bis zum Punkt $D_2$ auf $a$. Dann laufe man parallel zu $c$ zum Punkt $D_3$ auf der Seite $b$. Wiederholt man den gleichen Vorgang mit $D_3$ an Stelle von $D_0$, so erhält man Punkte $D_4$ auf $c$, $D_5$ auf $a$ und $D_6$ auf $b$. Es gilt $D_6=D_0$, das heisst, man kehrt nach sechs solchen Schritten zum Ausgangspunkt $D_0$ zurück.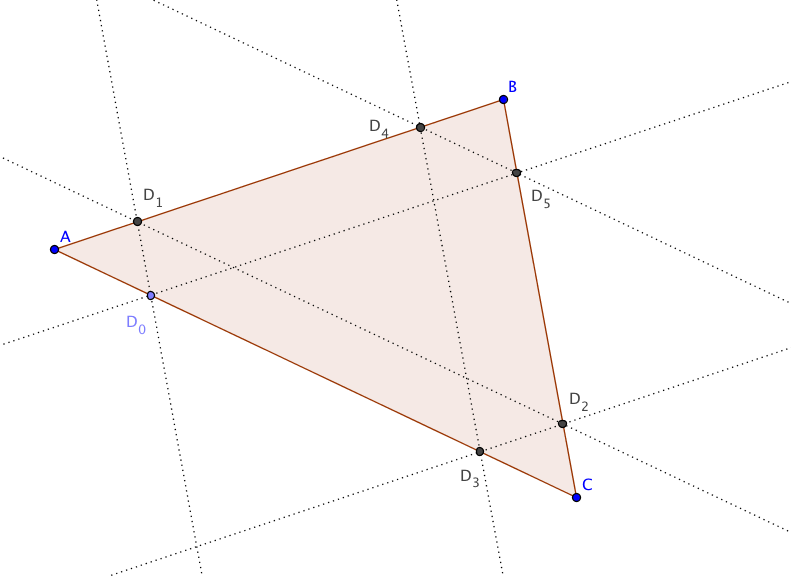
Denn: In der Tat ist die Abbildung $f: b \rightarrow b$, welche $D_0 $ auf $
D_6$ abbildet, eine Komposition von sechs Parallelprojektionen, also eine affine Abbildung. Diese bildet die Punkte $A$ und $C$ jeweils auf sich ab. Wegen (5.1) muss sie mit der identischen Abbildung übereinstimmen.