Satz des Menelaos 5.6. Es sei $ABC$ ein Dreieck. Es sei $A' \in BC$, $B' \in AC$ und $C' \in AB$. Keiner der Punkte $A',B',C'$ sei Eckpunkt des Dreiecks. Dann liegen die drei Punkte genau dann auf einer Geraden, wenn das folgende Produkt von Teilverhältnissen gleich $1$ ist
\begin{equation}
\frac{\overset{\longrightarrow}{A'B}}{\overset{\longrightarrow}{A'C}}\cdot \frac{\overset{\longrightarrow}{B'C}}{\overset{\longrightarrow}{B'A}}\cdot \frac{\overset{\longrightarrow}{C'A}}{\overset{\longrightarrow}{C'B}}=1.
\end{equation}
Beweis. Angenommen die Punkte $A', B', C'$ liegen auf einer Geraden $g$. Man zeichne zu $AB$ die Parallele durch $C$. Sie schneide $g$ im Punkt $D$. Dann findet man nach dem zweiten Strahlensatz die Gleichungen:
$$
\frac{\overset{\longrightarrow}{A'B}}{\overset{\longrightarrow}{A'C}} =
\frac{\overset{\longrightarrow}{C'B}}{\overset{\longrightarrow}{DC}},
\qquad
\frac{\overset{\longrightarrow}{B'C}}{\overset{\longrightarrow}{B'A}} =
\frac{\overset{\longrightarrow}{DC}}{\overset{\longrightarrow}{C'A}}.
$$ 
Multiplikation der Gleichungen liefert
$$
\frac{\overset{\longrightarrow}{A'B}}{\overset{\longrightarrow}{A'C}}
\cdot
\frac{\overset{\longrightarrow}{B'C}}{\overset{\longrightarrow}{B'A}} =
\frac{\overset{\longrightarrow}{C'B}}{\overset{\longrightarrow}{DC}}
\cdot
\frac{\overset{\longrightarrow}{DC}}{\overset{\longrightarrow}{C'A}}
=
\left(\frac{\overset{\longrightarrow}{C'A}}{\overset{\longrightarrow}{C'B}}\right)^{-1}.
$$ Es folgt die behauptete Formel.
Die Umkehrung erhält man, indem man den Schnittpunkt $A''$ der Geraden $B'C'$ mit der Gerade $BC$ betrachtet. Nach dem bereits Bewiesenem folgt die Gleichung
$$
\frac{\overset{\longrightarrow}{A''B}}{\overset{\longrightarrow}{A''C}}= \frac{\overset{\longrightarrow}{A'B}}{\overset{\longrightarrow}{A'C}}
$$ und damit $A''=A'$. Das heisst, die drei Punkte $A',B',C'$ liegen auf einer Geraden (vergleiche die erste Bemerkung zu Anfang des Kapitels).
qed.
Das im Satz von Menelaos auftretende Produkt $$ \frac{\overset{\longrightarrow}{A'B}}{\overset{\longrightarrow}{A'C}}\cdot \frac{\overset{\longrightarrow}{B'C}}{\overset{\longrightarrow}{B'A}}\cdot \frac{\overset{\longrightarrow}{C'A}}{\overset{\longrightarrow}{C'B}}$$ nennt man den Ceva-Menelaos Quotienten.
Satz des Ceva 5.7. Es sei $ABC$ ein Dreieck. Es seien $A' \in BC$, $B' \in AC$ und $C' \in
AB$. Keiner der Punkte $A',B',C'$ sei Eckpunkt des Dreiecks. Die drei Geraden $AA'$, $BB'$, $CC'$ schneiden sich genau dann in einem Punkt oder sind parallel, wenn gilt
\begin{equation}
\frac{\overset{\longrightarrow}{A'B}}{\overset{\longrightarrow}{A'C}}\cdot \frac{\overset{\longrightarrow}{B'C}}{\overset{\longrightarrow}{B'A}}\cdot \frac{\overset{\longrightarrow}{C'A}}{\overset{\longrightarrow}{C'B}}= - 1
\end{equation}
Beweis. Wir zeigen: Schneiden sich die drei Geraden in einem Punkt oder sind sie parallel, so ist der Ceva-Menelaos Quotient gleich $-1$.
Die Umkehrung, nämlich dass aus einem Ceva-Menelos Quotienten gleich $-1$ folge, die drei Geraden seien parallel oder schnitten sich in einem Punkt, wird analog zur Argumentation im Satz des Menelaos bewiesen und in den Übungen behandelt.
Zunächst nehmen wir an, dass sich die drei Geraden in einem Punkt $S$ schneiden.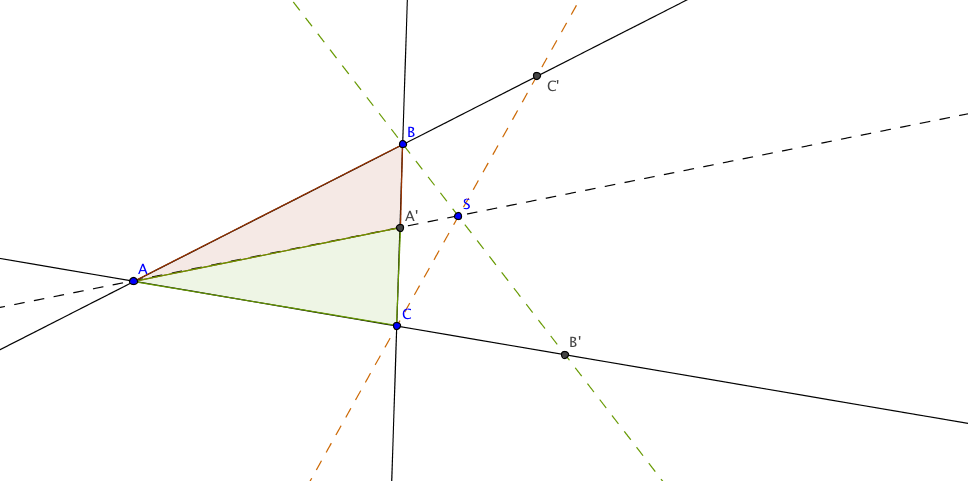
Wenden wir den Satz des Menelaos auf das Dreieck $ABA'$ an, so erhalten wir:
$$ \frac{\overset{\longrightarrow}{CB}}{\overset{\longrightarrow}{CA'}}\cdot \frac{\overset{\longrightarrow}{SA'}}{\overset{\longrightarrow}{SA}}\cdot \frac{\overset{\longrightarrow}{C'A}}{\overset{\longrightarrow}{C'B}} =1.
$$ Wenden wir den Satz des Menelaos auf das Dreieck $AA'C$ an, so erhalten wir:
$$ \frac{\overset{\longrightarrow}{BA'}}{\overset{\longrightarrow}{BC}}\cdot \frac{\overset{\longrightarrow}{B'C}}{\overset{\longrightarrow}{B'A}}\cdot \frac{\overset{\longrightarrow}{SA}}{\overset{\longrightarrow}{SA'}}
=1.
$$ Wenn man die beiden Gleichungen miteinander multipliziert, so erhält man:
\begin{align*}
1&= \frac{\overset{\longrightarrow}{BA'}}{\overset{\longrightarrow}{BC}}\cdot \frac{\overset{\longrightarrow}{B'C}}{\overset{\longrightarrow}{B'A}}\cdot \frac{\overset{\longrightarrow}{SA}}{\overset{\longrightarrow}{SA'}}\cdot \frac{\overset{\longrightarrow}{CB}}{\overset{\longrightarrow}{CA'}}\cdot \frac{\overset{\longrightarrow}{SA'}}{\overset{\longrightarrow}{SA}}\cdot \frac{\overset{\longrightarrow}{C'A}}{\overset{\longrightarrow}{C'B}}\\
&=\left(\frac{\overset{\longrightarrow}{BA'}}{\overset{\longrightarrow}{BC}}\cdot \frac{\overset{\longrightarrow}{CB}}{\overset{\longrightarrow}{CA'}}\right)
\cdot
\left(\frac{\overset{\longrightarrow}{SA}}{\overset{\longrightarrow}{SA'}}\cdot \frac{\overset{\longrightarrow}{SA'}}{\overset{\longrightarrow}{SA}}\right)
\cdot
\left(\frac{\overset{\longrightarrow}{B'C}}{\overset{\longrightarrow}{B'A}}\cdot \frac{\overset{\longrightarrow}{C'A}}{\overset{\longrightarrow}{C'B}}\right)\\
&=\left(-\frac{\overset{\longrightarrow}{A'B}}{\overset{\longrightarrow}{A'C}}\right)
\cdot 1
\cdot
\left(\frac{\overset{\longrightarrow}{B'C}}{\overset{\longrightarrow}{B'A}}\cdot \frac{\overset{\longrightarrow}{C'A}}{\overset{\longrightarrow}{C'B}}\right)
\end{align*} In der zweiten Gleichung werden die Faktoren umgruppiert. In der dritten Gleichung wird gekürzt und drei Vektoren werden durch ihr Negatives ersetzt.
Nun nehmen wir an, dass die drei Geraden parallel sind.
Mittels des ersten Strahlensatzes erhalten wir die beiden Gleichungen
$$
\frac{\overset{\longrightarrow}{B'C}}{\overset{\longrightarrow}{B'A}}
=
\frac{\overset{\longrightarrow}{BC}}{\overset{\longrightarrow}{BA'}}
\qquad \text{ und }\qquad
\frac{\overset{\longrightarrow}{C'A}}{\overset{\longrightarrow}{C'B}}
=
\frac{\overset{\longrightarrow}{CA'}}{\overset{\longrightarrow}{CB}}.
$$ Eingesetzt in den Ceva-Menelaos Quotienten, erhält man:
\begin{align*}
\frac{\overset{\longrightarrow}{A'B}}{\overset{\longrightarrow}{A'C}}\cdot \frac{\overset{\longrightarrow}{B'C}}{\overset{\longrightarrow}{B'A}}\cdot \frac{\overset{\longrightarrow}{C'A}}{\overset{\longrightarrow}{C'B}} = \frac{\overset{\longrightarrow}{A'B}}{\overset{\longrightarrow}{A'C}}\cdot \frac{\overset{\longrightarrow}{BC}}{\overset{\longrightarrow}{BA'}}\cdot\frac{\overset{\longrightarrow}{CA'}}{\overset{\longrightarrow}{CB}}
=-1\end{align*} qed.
Hier sind zwei unmittelbare Folgerungen:
Satz 5.8. Es sei $ABC$ ein Dreieck und $A',B',C'$ die Mittelpunkte der Seiten $\overline{BC},\overline{CA},\overline{AB}$. Die Seitenhalbierenden $AA'$, $BB'$ und $CC'$ schneiden sich in einem Punkt.
Beweis. Jeder der Faktoren im Ceva-Menelaos Quotienten ist gleich $-1$.
qed.
Satz 5.9. Es sei $ABC$ ein Dreieck und $A',B',C'$ die Höhenfußpunkte auf den Seiten $\overline{BC},\overline{CA},\overline{AB}$. Die Höhen $AA'$, $BB'$ und $CC'$ schneiden sich in einem Punkt.
Die Höhen eines Dreiecks sind die Lote von den Eckpunkten auf die jeweils gegenüberliegende Seite.
Beweis. Wir müssen hier drei Fälle unterscheiden. Der erste und offensichtliche Fall ist der eines rechtwinkligen Dreiecks. Der Eckpunkt mit dem rechten Winkel ist Schnittpunkt der Höhen.
In den beiden anderen Fällen interessieren wir uns zuerst einmal nur für Vorzeichen.
Im zweiten Fall sind alle Winkel kleiner als $90°$. Dann liegen die Höhenfußpunkte auf den Seiten des Dreiecks.
Die in den einzelnen Faktoren des Ceva-Menelaos Quotienten auftauchenden Vektoren zeigen jeweils in entgegengesetzte Richtungen. Jeder der drei Faktoren ist negativ, also auch der Ceva-Menelaos Quotient selbst.
Im dritten Fall ist ein Winkel, sagen wir einmal im Punkte $C$, stumpf, also größer als $90°$. Dann liegen die beiden Fußpunkte $A'$ und $B'$ außerhalb des Dreiecks. Die dazugehörigen Faktoren im Ceva-Menelaos Quotienten sind positiv. Der Punkt $C'$ liegt auf der Strecke $\overline{AB}$ und liefert einen negativen Faktor.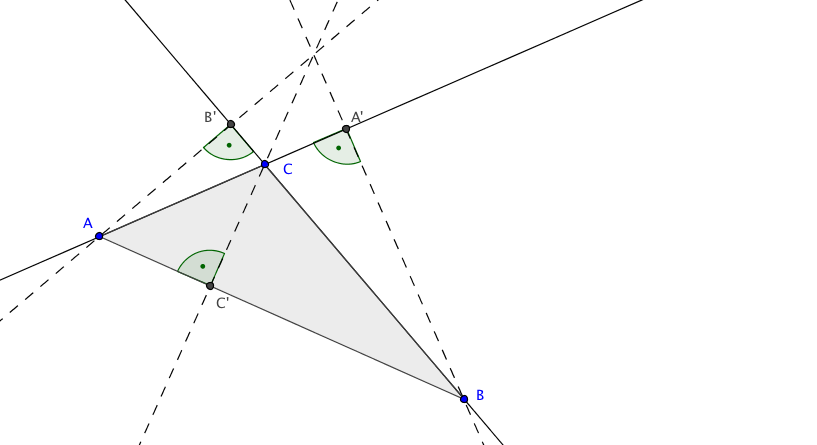
In beiden Fällen ist der Ceva-Menelaos Quotient negativ. Wir müssen nur den Betrag ausrechnen. Dazu betrachten wir einen Eckpunkt des Dreiecks, sagen wir einmal $A$, und die angrenzenden Höhenfußpunkte $B'$ und $C'$. Spiegelt man die Seite $AC$ an der Winkelhalbierenden bei $A$, so können wir den zweiten Strahlensatz anwenden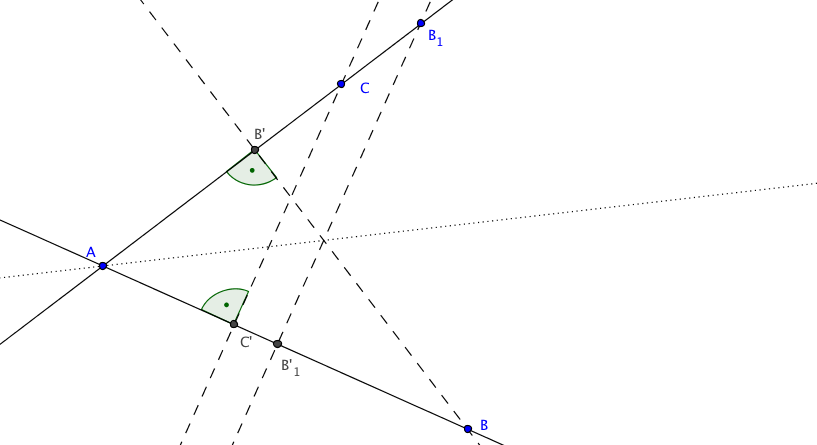
und erhalten $$\frac{|B'A|}{|C'A|}=\frac{|B'B|}{|C'C|}.$$ Der Betrag des Ceva-Menelaos Quotienten lässt sich folglich einfach berechnen:
\begin{align*}
\left| \frac{\overset{\longrightarrow}{A'B}}{\overset{\longrightarrow}{A'C}}\cdot \frac{\overset{\longrightarrow}{B'C}}{\overset{\longrightarrow}{B'A}}\cdot \frac{\overset{\longrightarrow}{C'A}}{\overset{\longrightarrow}{C'B}}\right|&=\frac{|A'B|}{|A'C|}\cdot\frac{|B'C|}{|B'A|}\cdot\frac{|C'A|}{|C'B|}
=\frac{|A'B|}{|C'B|}\cdot\frac{|B'C|}{|A'C|}\cdot\frac{|C'A|}{|B'A|}\\
&=\frac{|A'A|}{|C'C|}\cdot\frac{|B'B|}{|A'A|}\cdot\frac{|C'C|}{|B'B|}=1.
\end{align*} qed.
Satz 5.10. Es sei $ABC$ und $D$ der Schnittpunkt der Winkelhalbierenden in $A$ mit der Seite $\overline{BC}$. Dann gilt $$\frac{|AB|}{|AC|}=\frac{|DB|}{|DC|}.$$
Beweis. Wir betrachten die Parallele zu $AC$ durch den Punkt $B$. Diese schneidet die Winkelhalbierende $AD$ im Punkte $E$.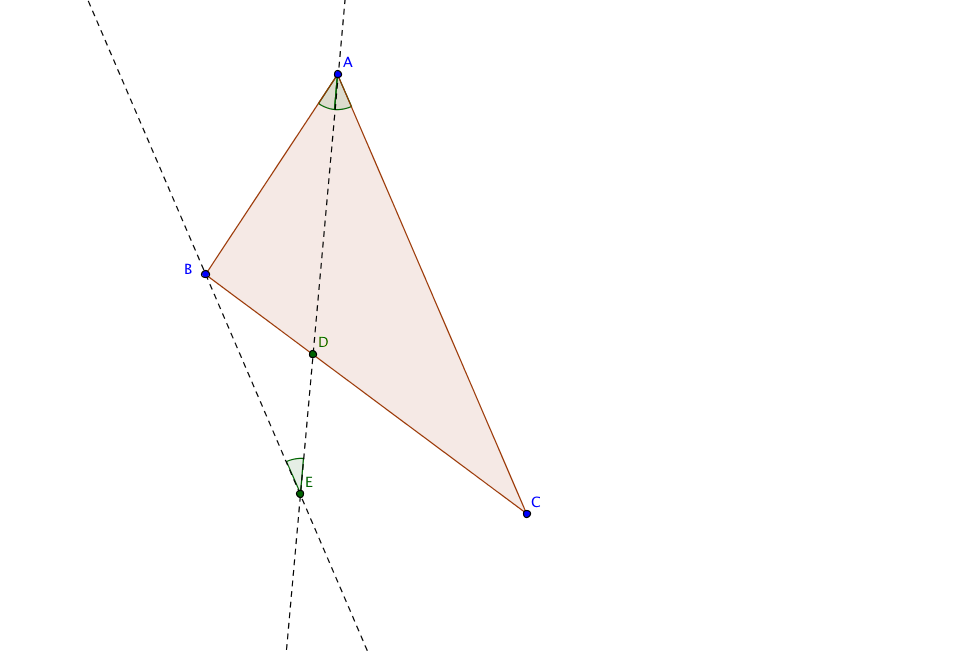
Die Winkel $\angle BED$ und $\angle CAD$ sind an parallelen Geraden, also gleich. Folglich sind die Dreiecke $BED$ und $CAD$ ähnlich und es gilt $$\frac{|DC|}{|AC|}=\frac{|DB|}{|BE|}.$$ Das Dreieck $ABE$ besitzt zwei gleiche Winkel, ist also gleichschenklig $$|BE|={|AB|}.$$ Eingesetz, folgt die behauptete Gleichung $$\frac{|AB|}{|AC|}=\frac{|DB|}{|DC|}.$$ qed.