Definition. Ein Viereck $ABCD$ heißt Parallelogramm, wenn gilt $AB \parallel CD$ und $BC \parallel DA$.
Es sei $T = \overset{\rightarrow}{AD}$ die Translation. Die Konstruktion (2.11) zeigt, dass $T(A) = D$ und $T(B) = C$ Durch eine Parallelverschiebung erkennt man leicht, dass sich nebeneinander liegende Innenwinkel zu $180°$ aufaddieren: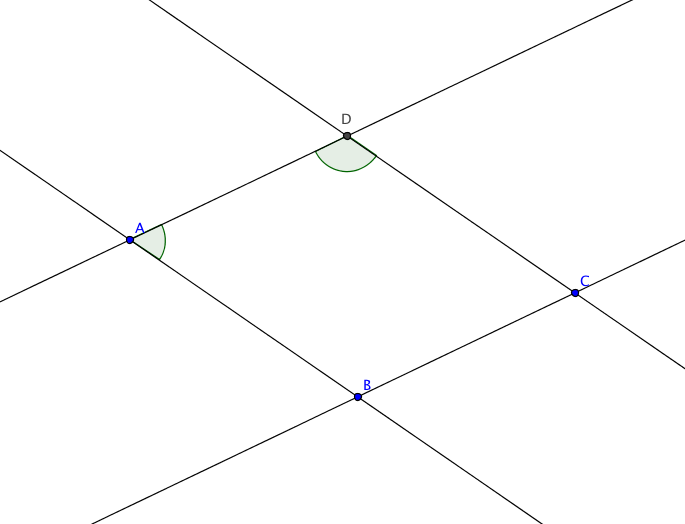
\begin{array}{l}
\sphericalangle BAD + \sphericalangle ADC = 180^{\circ}.\\
\sphericalangle ADC + \sphericalangle DCB = 180^{\circ}\\
\sphericalangle DCB + \sphericalangle CBA = 180^{\circ}\\
\sphericalangle CBA + \sphericalangle BAD = 180^{\circ}
\end{array} Es folgen die Gleichungen
\begin{array}{l}
\sphericalangle BAD = \sphericalangle DCB\\
\sphericalangle ADC = \sphericalangle CBA.
\end{array} Das Gleiche gilt für die geometrischen Winkel: Gegenüber liegende Winkel sind gleich und nebeneinander liegende Winkel ergänzen sich zu $180°$.
Aus den Eigenschaften der Translationen folgt, dass gegenüberliegende Seiten gleich lang sind.
$$
|AB| = |CD|, \quad |DA| = |BC|.
$$ In der Tat, gilt $|AB| = |T(A)T(B| =|DC|$. Folglich gibt es eine Bewegung $\rho$, so dass $\rho (C) = A$ und $\rho(D) = B$. Dann vertauscht $\rho \circ T$ die Endpunkte der Strecke $AB$ und ist daher eine Drehung um $180^{o}$. Da der Drehwinkel von $T$ null ist, ist auch $\rho$ eine Drehung um $180°$. Also ist $\rho^{2} = \mathrm{id}$. Wir erhalten
$$
\rho(A) = C, \quad \rho(B) = D.
$$ Wir sehen, dass $\rho$ eine Symmetrie des Parallelogramms ist, die die beiden Diagonalen festlässt. Der Fixpunkt $M$ von $\rho$ fällt also mit dem Mittelpunkt von jeder der beiden Diagonalen zusammen.
$$
|AM| = |CM|, \quad |DM| = |BM|.
$$ Man nennt $M$ den Mittelpunkt des Parallelogramms.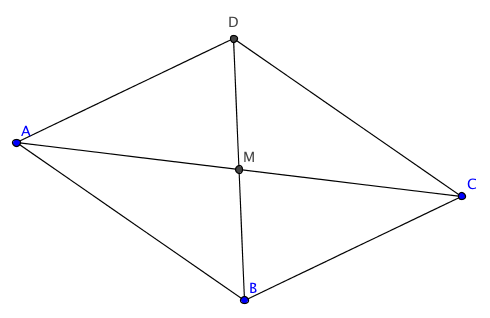
Proposition 4.1. Es sei $ABCD$ ein Viereck mit $|AB|=|CD|$ und $AB \parallel CD$. Dann ist $ABCD$ ein Parallelogramm.
Beweis. Es sei $T$ die Translation, welche den Mittelpunkt, der Strecke $\overline{AB}$ auf den Mittelpunkt der Strecke $\overline{CD}$ abbildet. Dann sind die Strecken $\overline{T(A)T(B)}$ und $\overline{CD}$ parallel, gleich lang und haben den gleichen Mittelpunkt. Also sind die Strecken gleich. Daher muss gelten:
$$
T(A) = D, \; T(B) = C \quad \text{oder} \; T(A) = C, \; T(B) = D.
$$ Wenn der erste Fall vorliegt, ist $ABCD$ ein Parallelogram. Im zweiten Fall ist $ABDC$ ein Parallelogramm. Wie wir schon bewiesen haben, würden sich dann die Diagonalen $\overline{AD}$ und $\overline{BC}$ schneiden. Das widerspricht der Annahme, dass $ABCD$ ein Viereck ist, dessen Seiten keine weiteren Schnittpunkte haben dürfen.
qed.
Proposition 4.2. Es sei $ABCD$ ein Viereck mit $|AB|=|CD|$ und $|AD|=|BC|$. Dann ist dies ein Parallelogramm.
Beweis. Man kann annehmen, dass $B$ und $D$ auf verschiedenen Seiten der Gerade $AC$ liegen. Da die Dreiecke $ABC$ und $CDA$ kongruent sind (SSS), gibt es eine Isometrie $\rho$,so dass
$$
\rho (A) = C, \quad \rho (B) = D, \quad \rho (C) = A.
$$ Also kann $\rho$ nur die Spieglung an der Mittelsenkrechten von $AC$ oder die Punktspieglung um den Mittelpunkt von $AC$ sein. Es kommt aber nur der letztere Fall in Frage, da $\rho $ die Seiten der Geraden $AC$ vertausschen muss. Hier benutzen wir die Annahme, dass $B$ und $D$ auf verschiedenen Seiten der Geraden $AC$ liegen. Da eine Punktspiegelung einer Gerade auf eine dazu parallele Gerade abbildet folgt die Behauptung.
qed.