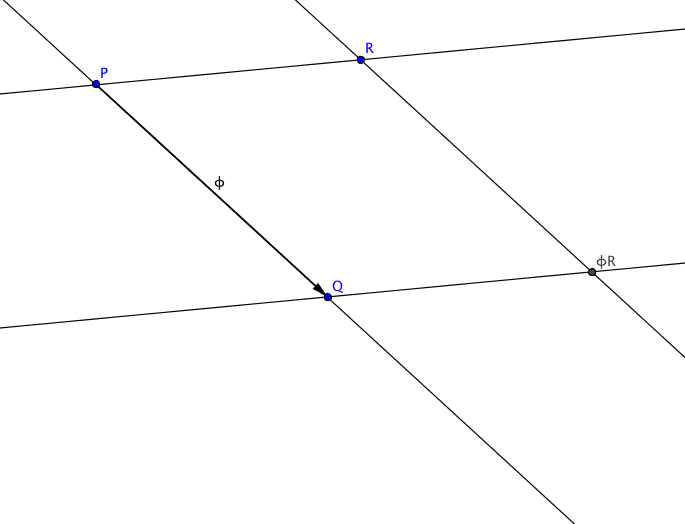
Konstruktion 2.11. Es seien $P\neq Q$ zwei Punkte und $\phi$ die durch den Vektor $\overset{\longrightarrow}{PQ}$ beschriebene Translation. Wir überlegen uns, wie wir zu einem gegebenen Punkt $R$ der Ebene das Translat $\phi(R)$ konstruieren können. Es sind zwei Fälle zu unterscheiden.
- Sei $R\notin PQ$. Nach Satz (2.10) gilt $PR\parallel\phi(P)\phi(R)$, der Punkt $\phi(R)$ liegt also auf der Parallelen zu $PR$ durch $\phi(P)=Q$. Die beiden Geraden $P\phi(P)=PQ$ und $R\phi(R)$ sind invariant, also parallel. Folglich liegt $\phi(R)$ auf der Parallelen zu $PQ$ durch $R$. Der Punkt $\phi(R)$ ist also der Schnittpunkt der Parallelen zu $PQ$ durch $R$ und der Parallelen zu $PR$ durch $Q$.
- Ist $R\in PQ$, so fallen die Geraden $PQ$ und $PR$ zusammen und die obige Konstruktionsvorschrift liefert keinen eindeutig bestimmten Punkt. Wir können uns aber mit einem kleinen Trick wieder in die obige Situation versetzen. Dazu wählen wir einen beliebigen Punkt $P'$, der nicht auf der Geraden $PQ$ liegt und konstruieren wie zuvor $Q'=\phi(P')$. Wegen der Gleichheit der Vektoren $\overset{\longrightarrow}{PQ}=\overset{\longrightarrow}{P'Q'}$ liefert die obige Konstruktion nun $\phi(R)$ als Schnittpunkt der Parallelen zu $P'Q'$ durch $R$ und der Parallelen zu $P'R$ durch $Q'$.
Im Beweis der nächsten Proposition brauchen wir eine Aussage, die von der Anschauung her offensichtlich erscheint. Der Beweis benutzt das Parallelenaxiom. Wie ich andernorts bereits bemerkte, gibt es andere Geometrieen als die ebene euklidische, in denen das Parallelenaxiom nicht gilt. Insbesondere in der hyperbolischen Geometrie ist die folgende Aussage nicht wahr.
Bemerkung. Seien $g,h,k$ Geraden in der Ebene. Gilt $g\parallel h$ und $h\parallel k$, so gilt auch $g\parallel k$.
Beweis. Wir nehmen an, $P$ sei ein Schnittpunkt der Geraden $g$ und $k$. Nach dem Parallelenaxiom gibt es durch $P$ genau eine Parallele zu $h$. Es sind aber sowohl $g$ als auch $k$ Parallelen zu $h$, die durch den Punkt $P$ gehen. Folglich muss gelten $g=k$.
qed.
Proposition 2.12. Sind $\phi$ und $\psi$ Translationen, so auch $\phi\circ\psi$ und $\psi\circ\phi$ und es gilt: $ \phi\circ\psi=\psi\circ\phi$.
Beweis. Ist $\phi$ oder $\psi$ die Identität, so ist nichts zu zeigen. Andernfalls bilden sowohl $ \phi$ als auch $\psi$ Geraden jeweils auf dazu parallele Geraden ab. Da Parallelität transitiv ist, bildet auch $\chi=\phi\circ\psi$ Geraden auf dazu parallele Geraden ab. Sei $P\in\mathbb{E}$ gegeben und $\chi(P)\not=P$. Das Bild der Geraden $P\chi(P)$ bei $\chi$ ist dann parallel zu $P\chi(P)$ und enthält den Punkt $\chi(P)$. Also ist die Gerade $P\chi(P)$ invariant unter $\chi$. Zu zeigen bleibt, dass $\chi$ keine Punktspiegelung ist. Dann gäbe es einen Fixpunkt $Q$ auf $P\chi(P)$, also $\phi\left(\psi(Q)\right)=Q$. Dann wäre $\phi=\overset{\rightarrow}{\psi(Q)Q}$ und $\psi=\overset{\rightarrow}{Q\psi(Q)}$ Umkehrabbildungen voneinander und folglich $\phi\circ\psi$ die Identität, eine Translation.
Um die Gleichung $ \phi\circ\psi=\psi\circ\phi$ zu verifizieren, unterscheiden wir zwei Fälle. Im ersten Fall seien die invarianten Geraden von $ \phi$ und $\psi$ nicht parallel. Entsprechend der Konstruktion (2.11) ist für einen gegebenen Punkt $P\in\mathbb{E}$ der Bildpunkt $\psi\left(\phi(P)\right)$ Schnittpunkt der zu $P\phi(P)$ parallelen Geraden durch $\psi(P)$ und der zu $P\psi(P)$ parallelen Geraden durch $\phi(P)$. Der Punkt $\phi\left(\psi(P)\right)$ ist der Schnittpunkt derselben beiden Geraden. Somit stimmen für beliebige Punkte $P\in\mathbb{E}$ die Bilder $\psi\circ\phi(P)$ und $\phi\circ\psi(P)$ überein. Folglich gilt $ \psi\circ\phi=\phi\circ\psi$. 
Im zweiten Fall sind die invarianten Geraden von $\phi$ und $\psi$ parallel. Wir wählen eine weitere Translation $\chi$, deren invariante Gerade nicht parallel ist zu den invarianten Geraden von $\phi$ und $\psi$. In der Gleichungskette \begin{array}{rcl}
\chi\circ(\phi\circ\psi) & = & (\chi\circ\phi)\circ\psi\\
&= & (\phi\circ\chi)\circ\psi\\
& = & \phi\circ(\chi\circ\psi)\\
&= & (\chi\circ\psi)\circ\phi\\
& = & \chi\circ(\psi\circ\phi)
\end{array} benutzen wir abwechselnd die Assoziativität von Abbildungen (d.h. wir können beliebig umklammern) und den bereits bewiesenen ersten Fall. Insgesamt folgt $\psi\circ\phi=\phi\circ\psi$ und mit der Umkehrabbildung $\chi^{-1}$ erhalten wir $$
\psi\circ\phi=\chi^{-1}\circ\chi\circ\psi\circ\phi=\chi^{-1}\circ\chi\circ\phi\circ\psi=\phi\circ\psi.$$qed.
Notation. Bei Translationen bezeichnet man das Kompositum meist mit $+$ statt mit $\circ$, man schreibt also $S+T=S\circ T$. Die identische Abbildung $\mathrm{id}$, betrachtet als Translation, wird dann als Nullvektor bezeichnet, $\mathrm{id}=\overset{\rightarrow}{0}.$ Mit dieser Bezeichnung gilt: $$T+\overset{\rightarrow}{0}=T.$$ Für beliebige Punkte $P,Q,R$ gilt die Additionsformel $$\overset{\longrightarrow}{PQ}+\overset{\longrightarrow}{QR}=\overset{\longrightarrow}{PR}.$$