Drachenviereck

Definition. Ein Viereck $ABCD$ heißt ein Drachenviereck, wenn gilt
$$
|AB| = |AD|, \quad |CB| = |CD|.
$$

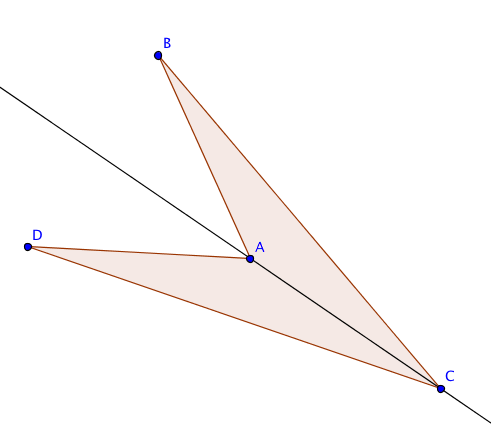
Es folgt nach SSS, dass die Dreiecke $ACB$ und $ACD$ kongruent sind. Also gibt es eine eindeutig bestimmte Isometrie $s$, so dass
$$
s(A) = A, \; s(C) = C \; s(B) = D
$$ Aus den ersten beiden Gleichung folgt, dass $s$ nur die Spieglung an der Geraden $AC$ sein kann und $s(D) = B$ gilt. Als Konsequenz erhält man:

1. Die Winkel bei $B$ und $D$ sind gleich.
2. Die Diagonalen $\overline{AC}$ und $\overline{BD}$ stehen senkrecht zueinander.
3. Die Spiegelachse $AC$ halbiert die Strecke $\overline{BD}$, und
4. halbiert ebenso die Winkel bei $A$ und $C$.

Definition. Ein Viereck $ABCD$ heißt Rhombus oder Raute, wenn alle vier Seiten gleich lang sind.

Ein Rhombus ist gleichzeitig Parallelogramm und Drachenviereck. Eine Raute besitzt vier Symmetrien: Die beiden Spiegelungen an den Winkelhalbierenden, die Identität und die Punktspiegelung am Mittelpunkt.

Definition. Ein Quadrat ist gleichzeitig Rhombus und Rechteck.

Ein Quadrat besitzt $8$ Symmetrien, nämlich $2$ Spiegelungen an den Mittelsenkrechten der Seiten und $2$ Spiegelungen an den Winkelhalbierenden, sowie die $4$ Drehungen um den Punkt $M$ um die Drehwinkel $0°$, $90°$, $180°$, bzw. $270°$.