Definition. Ein Rechteck ist ein Parallelogramm $ABCD$, dessen Winkel $90°$ haben:
\begin{equation}
\angle CAB = \angle ABD = \angle BDC = \angle CDA = 90^{\circ}
\end{equation}
Es genügt, dass einer der Winkel $90^{\circ}$ hat. Dies folgt aus den Eigenschaften der Winkel in einem Parallelogramm: Nebeneinander liegende Winkel ergänzen sich zu $180°$.
Da die Dreiecke $ABD$ und $BAC$ nach (SWS) kongruent sind, gibt es eine Isometrie $\sigma$, so dass $\sigma (A) = B$, $\sigma (B) = A$ und $\sigma (D) = C$. Da $\sigma$ die Seiten der Geraden $AB$ respektiert muss $\sigma$ die Spieglung um die Mittelsenkrechte $h$ von $AB$ sein. Weil $\sigma (D) = C$ ist, fällt diese Mittelsenkrechte mit der von $CD$ zusammen. Das ist die Achse von $\sigma$. Da $\sigma$ die beiden Diagonalen vertauscht, sind die Diagonalen in einem Rechteck gleich lang. Der Schnittpunkt $M$ der Diagonalen muss auf der Achse von $\sigma $ liegen.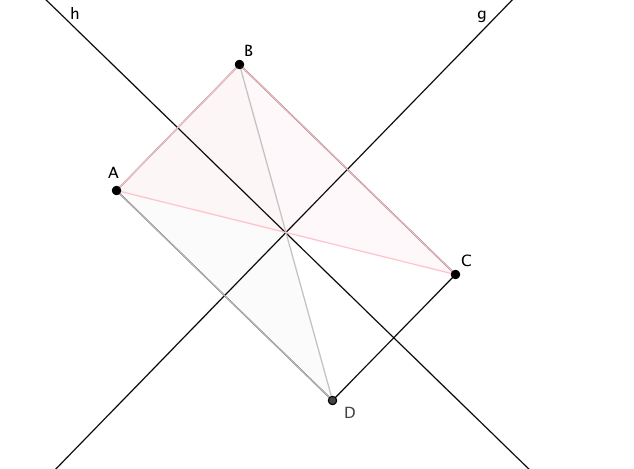
Ein Rechteck hat folglich $4$ Symmetrien. Die Identität, die Spiegelungen um die Mittelsenkrechten $h$ und $g$ von $\overline{AB}$ und $\overline{BC}$, sowie die Punktspiegelung um den Mittelpunkt $M$. Wendet man diese vier Symmetrien auf die Strecke $\overline{AM}$ an, so erhält man:
Proposition 4.3. Es sei $ABCD$ ein Rechteck und es sei $M$ der Schnittpunkt der Diagonalen. Dann gilt: \begin{equation}
|MA| = |MB| = |MC| = |MD|\end{equation}
Satz von Thales rückwärts 4.4. Es sei $ABC$ ein rechtwinkliges Dreieck mit der Hypotenuse $AC$. Es sei $M$ der Mittelpunkt von $\overline{AC}$. Dann gilt $|MB|=|MA|=|MC|$.
Beweis. Die Punktspiegelung $\rho$ an $M$ bildet $B$ auf $D = \rho(B)$ ab. Da eine Punktspieglung jede Gerade auf eine zur ihr parallele Gerade abbildet, ist $ABCD$ ein Parallelogramm mit einem rechten Winkel. Die Behauptung folgt aus (4.4).
qed.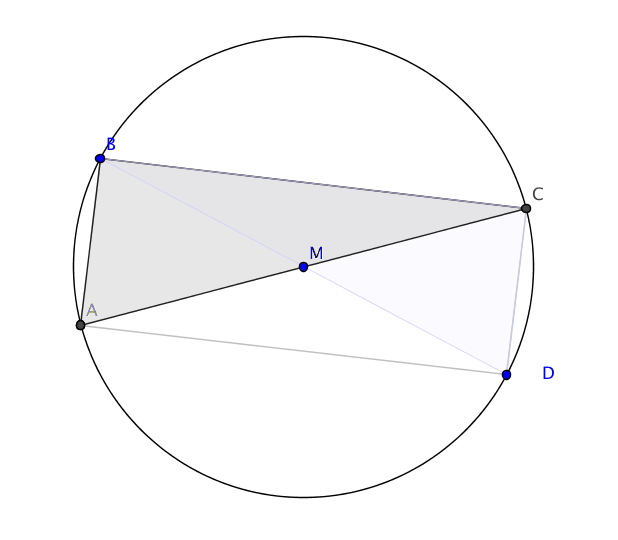
Satz von Thales vorwärts 4.5. Es sei $ABC$ ein Dreieck und $M$ der Mittelpunkt von $\overline{AC}$. Wenn $|MB|=|MA|=|MC|$, so ist $\angle
ABC$ ein rechter Winkel.
Beweis. Die Punktspieglung $\rho$ an $M$ liefert ein Parallelogramm $ABCD$ mit zwei gleich langen Diagonalen ($D = \rho (B)$). Dann sind die Dreiecke $CDB$ und $BAC$ kongruent. Wir finden eine Isometrie $s$ mit $s(C) = B$, $s(D) = A$ und $s(B) = C$. Dann muss $s$ die Spieglung um die Mittelsenkrechte von $BC$ sein. Also ist $ABCD$ ein Rechteck.
qed.
Der Beweis zeigt die folgende äquivalente Formulierung.
Korollar 4.6. Ein Parallelogramm, dessen Diagonalen gleich lang sind ist ein Rechteck.